线性回归分析
一 定义：回归分析（Regression Analysis）是一种统计学上的分析数据的方法，目的在于了解两个或多个变量之间是否相关以及相关方向与强度，并建立数学模型以便观察特定的自变量与需要预测的因变量之间的关系。具体的说，回归分析可以帮助了解在一个或多个自变量变化时因变量的变化量。
二 回归问题的分析方法：1）收集数据；2）建立一个适合相关问题的回归函数；3）通过学习已有的数据，对函数的未知参数进行估计；3）回归方程及回归系数的显著性检验；4）利用这个模型去预测/分类新的数据。
三 回归分析的原理：目的是为了找出一个最能够代表所有观测资料的函数，用这个函数来表示因变量与自变量的关系。回归的基本模型一般可以表示为：Y=f(X ,u)，其中Y为因变量，X为自变量，u为未知参数。
四 回归分析方法分类：根据用途可以有多种分类，单变量的线性回归模型，多变量的线性回归模型，广义线性回归模型，概率单位回归模型，逻辑回归模型，曲线回归模型，岭回归模型，主成分回归模型等。
五 回归分析算法背景：
回归分析核心思想是采用最小二乘法原理来求解回归系数，最小二乘法思想背景：1801年，意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。经过40天的跟踪观测后，由于谷神星运行至太阳背后，使得皮亚齐失去了谷神星的位置。随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星，但是根据大多数人计算的结果来寻找谷神星都没有结果。时年24岁的高斯计算了谷神星的轨道并进行了分析。奥地利天文学家海因里希·奥伯斯根据高斯计算出来的轨道重新发现了谷神星。
高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》中，而法国科学家勒让德于1806年独立发现“最小二乘法”，但因不为世人所知而默默无闻。两人曾为谁最早创立最小二乘法原理发生争执。
1829年，高斯提供了最小二乘法的优化效果强于其他方法的证明，见高斯-马尔可夫定理。
六 参考资料：
· 中央大学数学系教材-最小二乘法
· 最小二乘法 - 维基百科，自由的百科全书
· http://www.physics.csbsju.edu/stats/least_squares.html
· http://www.orbitals.com/self/least/least.htm
· PlanetMath上最小二乘法
· 马克威分析系统使用教程——http：//www.tenly.com
1.1 算法摘要
线性回归分析（Linear regression）是利用函数对一个或多个自变量和因变量之间进行建模的一种回归分析。这个函数是由模型的一个或多个回归系数组成的线性组合。当回归模型中仅有一个自变量的情况称为一元回归，当解释变量超过一个的情况称为多元回归。根据模型对参数是否为线性可以将模型分为线性模型和非线性模型。
对数据进行线性回归分析应注意事项：样本量不得少于30条记录；自变量和因变量都应该是连续性数值型变量；对多分类线性回归问题，分类等级变量可用哑变量方法加以分解，其中哑变量的主要目的是把多分类自变量处理成近似于二分类变量的样子。
1.2 算法原理
线性回归模型有几个基本的假设，自变量之间无多重共线性；随机误差服从均值为0，方差相同的正态分布；随机误差之间无相关关系。对线性回归模型的参数估计一般用最小二乘法进行估计。为了检验模型的拟合程度，对参数可用t检验，对整体模型的检验可用F检验，同时还可通过R平方和修正的R平方判断线性回归模型的拟合程度。下面简要的讨论一元和多元回归模型的表达式及参数估计方法。
A 一元线性回归分析
一元线性回归分析的回归方程的基本表达式为：
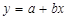
此方程在几何上表示一条直线，因此，称它为y 对x的回归直线，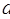
为截距，
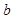为斜率，线性回归分析主要对回归方程的斜率和截距进行估计；其估计的方程为：
，
，
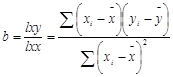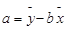其中：
线性回归模型的随机误差应该服从正态分布；且自变量之间没有多重共线性；随机误差项之间没有相关关联。所以在回归分析预测法中，需要对X和Y之间的相关程度作出判断，这就要计算两者之间的相关系数r，计算公式如下：
当r＝0时，表示不存在线性相关；当0＜r≤0.3时，为微弱相关；当0.3＜r≤0.5时，为低度相关；当0.5＜r≤0.8时，为显著相关；当0.8＜r<1时，为高度相关；当r＝1时，为完全线性相关。
对参数的估计可以使用最小二乘法进行估计。
B 多元线性回归分析
多元线性回归预测模型的一般公式为：
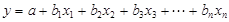
多元线性回归模型中最简单的就是只有两个自变量的二元线性回归模型，其一般形式为：
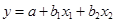
下面以二元线性回归分析为例，说明多元回归分析预测的系数估计方法。二元线性回归对系数的估计主要通过求解以下方程得到：
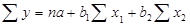
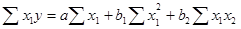
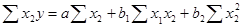三相关应用
线性回归分析是对客观事物数量关系的分析，是一种重要的统计分析方法，被广泛的应用于金融领域、计量经济学、财政税收预测等领域。其中在金融行业中，资本资产定价模型可以利用线性回归以及Beta系数的概念分析计算投资的系统风险；在经济学中，线性回归是主要的实证工具。例如，它是用来预测消费支出，固定投资支出，存货投资，出口产品的购买，进口支出，要求持有流动性资产，劳动力需求，劳动力供给等指标。
线性回归是回归分析中第一种经过严格研究并在实际中广泛应用的回归类型。这是因为线性的未知参数估计模型比非线性未知参数估计模型更容易拟合，而且产生的估计参数的统计特征也更容易确定。
线性回归有很多实际用途；分为以下两大类：
1）如果目标是预测或者映射，线性回归可以用来对观测数据集Y和X的值拟合出一个预测模型。当完成这样一个模型以后，对于一个新增的X值，在没有给定与它相配对的Y的情况下，可以用这个拟合过的模型预测出一个Y值。
2）给定一个变量Y和一些变量X1,...,XP，这些变量有可能与Y相关，线性回归分析可以用来量化Y与Xj之间相关性的强度，评估出与Y不相关的Xj，并识别出哪些Xj的子集包含了关于Y的冗余信息。
四参考资料1 线性回归预测法 - MBA智库百科
2 何晓群，关于中国统计学科建设的若干思考.北京：统计研究，1996（2）
3 何晓群，现代统计分析方法与应用（第二版）.北京：2007.8
4 回归分析 - 维基百科，自由的百科全书
5 马克威分析系统使用教程——http：//www.tenly.com
五实例下面举一个实例来检验一元线性回归分析。假设有10个同类企业的生产性固定资产价值和工业总产值数据如下：
| 生产性固定资产价值（万元） | 工业总产值（万元） |
| 318 | 524 |
| 910 | 1019 |
| 200 | 638 |
| 409 | 815 |
| 415 | 913 |
| 502 | 928 |
| 314 | 605 |
| 1210 | 1516 |
| 1022 | 1219 |
| 1225 | 1624 |
现在试求出两者的相关关系，以及回归方程。
假设工业总产值为Y，生产性固定资产价值为x，并且两个变量的回归方程为：Y=a+bx
首先计算两者的相关系数r，通过相关系数的公式计算得到r=0.9478；这说明两者之间存在高度强相关关系，认为自变量的变化对因变量的影响非常大。最后计算得到两个变量的回归方程为：
工业总产值=395.567+0.896*生产性固定资产投资
表明生产性固定资产投资每增加1单位，工业总产值增加0.896个单位值。
六输入输出输入变量类型：整型、浮点型
输入数据尺度：标量型
输出结果：得到线性回归模型中自变量和因变量之间的回归方程。
七相关条目相关分析、多元统计分析、最小二乘法
八优缺点优点：一元线性回归模型虽然比简单，但是它的统计思想非常重要。多元统计分析是一元线性回归结果的直接推广，线性回归分析的应用非常广泛，只要具有相关关系的变量，就可以进行回归分析。
缺点：对数据要求较高，须具有正态分布的特点，数据之间不能有多重共线性，回归模型及回归系数需进行系数检验、残差检验与稳定性检验。另外，在实际问题中回归方程并非严格的直线，此时用回归方程去预测可能导致较大的误差。
十外部链接解读回归分析的原理及结构
http://molecular-service-science.com/2012/09/statistics-regression/