马克威向量自回归
马克威操作说明
以数据文件“马克威通用数据2.mkw”为例,演示向量自回归模型算法的操作。数据为记录了四支股票293个交易日的有关数据,试用移动平均模型来预测股票一在其后若干交易日的数据。
(1)首先,在工作区,打开建模分析工作流“高级统计”→“向量自回归”;
(2)接着选择数据源;
(3)然后设置算法的参数;
(4)主要的操作步骤如下:
1)选择数据源;
2)变量选择:
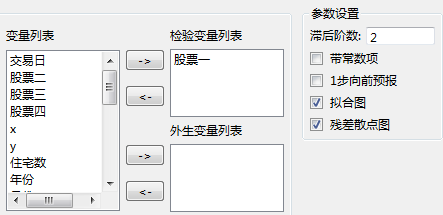
检验变量列表:选入要分析的变量名。
外生变量列表:在模型中增加一个(或多个)外生变量。
滞后阶数:写入自回归阶数,要求为正整数。
带常数项:指定模型中包含常数项。
1步向前预报:输出1步向前预测的结果,当模型不含外生变量时有效。
拟合图:输出拟合图。
残差散点图:输出残差散点图。
参数设置如下所示,检验变量选择“股票一”,滞后阶数为2阶:
(5)输出结果:
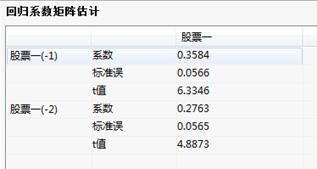
回归系数矩阵估计:
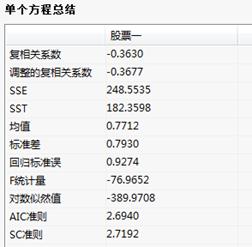
单个方程总结:
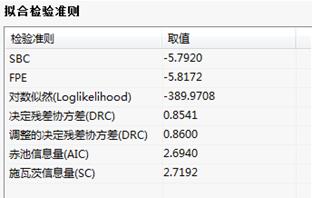
拟合检验准则:
(6)结果说明:
回归系数矩阵估计表输出自回归变量股票一的回归参数;
单个方程总结表输出对于单个模型的总结统计量,包括了各个复相关系数,调整复相关系数,以及每个模型的SSE、SST、因变量均值和标准差;
拟合检验准则表输出整个向量自回归模型拟合的优劣准则,包括SBC、FPE、对数似然、决定残差协方差、赤池信息量和施瓦茨信息量等,其中AIC、SC信息量的值越小说明模型的拟合效果越好,因此在实际检验中,应尽量选择信息量较小的模型。
数据要求
输入变量类型:要求数值型变量;
算法用途
向量自回归用于描述一个多维向量的各个分量的自回归关系,不仅包括各个分量对自身滞后项的关系,还包括某个分量与其他分量滞后项之间的关系。
向量自回归常用于预测相互联系的时间序列系统以及分析随机扰动对变量系统的动态影响,可用于分析不同类型的随机误差项对系统变量的动态影响;当变量之间不仅存在滞后影响,而且存在同期影响关系时,适合建立向量自回归模型;综合来说向量自回归可用于分析能用向量性质分析的各个领域的数据。
算法原理
通过计算各变量的回归系数矩阵估计变量与其他滞后项的关系。主要的模型和参数估计方法为:
假设原始数据 的均值为非零数
的均值为非零数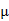 ,同时可经过线性变换令
,同时可经过线性变换令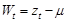 ;将原始数据集变为新的数据集
;将原始数据集变为新的数据集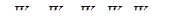 ;这个数据的向量自回归模型可表示为:
;这个数据的向量自回归模型可表示为:
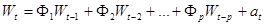
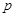 阶自回归模型
阶自回归模型
参数估计可通过计算样本自协方差函数、样本自相关系数和样本偏自相关函数得到:
样本自协方差函数:
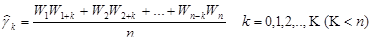
样本自相关系数:
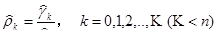
样本偏自相关函数:
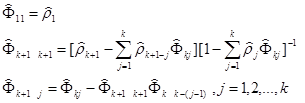
结果与解释
输出结果:
回归系数矩阵表:给出变量之间的回归系数矩阵值;
单个方程总结表:给出变量的复相关系数、调整复相关系数、均值、标准误差等统计量;
拟合检验准则:给出拟合数据的标准准则的值;其中AIC、SC信息量越小说明模型的拟合效果越好,因此在实际检验中,应尽量选择信息量较小的模型。
图表:给出变量的残差图和拟合图。
| 订购用户 | 订购时间 |
| 1355****728 | 2022-03-24 10:55:00 |
| 1389****716 | 2020-05-26 13:30:17 |
| 1391****799 | 2019-03-31 13:50:15 |
| 1526****123 | 2019-03-23 20:44:52 |
| 1526****123 | 2019-03-23 20:37:42 |
| 1811****398 | 2018-07-23 13:46:24 |
| 1552****998 | 2018-04-07 00:58:49 |
| 1398****741 | 2017-12-29 09:10:30 |
| 1556****001 | 2017-08-10 23:45:25 |
| 1364****964 | 2017-06-19 16:00:07 |
| 第1页 | |
