
(1)以数据文件“马克威通用数据1.mkw”为例,演示双样本比例检验算法的操作。
首先,在工作区内,打开建模分析工作流:“基础分析→参数检验→双样本比例检验”,接着选择数据源,然后设置算法的参数,最后点击运行按钮。
其中各类参数的含义如下:
变量表:在选入变量时,若不使用分组变量,需要同时选中两个变量方能添加至“已选变量表”。
分组变量:用来把参与运算的样本进行分组的变量。如果需要比较的数据为两个不同的变量,则不需要使用分组变量,直接选中两个变量,添加到变量表。
分组参数定义:分组参数定义包括指定分组值法和指定分界值法。
指定分组值法:一般应用于二值型、布尔型和整型的数据。指定的两个不同的取值,将样本分成两个组。分组值要求设置为分组变量的一个固定取值。
指定分界值法:一般应用于连续型数据。分界值将全部观测量按分组变量值大于等于分界值和小于分界值分成两个组。分界要求设置为分组变量的最小值和最大值之间的任意一个实数。
置信度:设置置信度的值,要求为区间(0,1]之间任意值,系统默认为95%。
原假设:p1=p2,一般用H0表示。
备择假设:双侧检验的备择假设为:p1≠p2;单侧检验的备择假设为:p1>p2或p1<p2。
区间估计:双侧置信区间的估计采用点估计法。
合并样本基础上估计的比例P:合并样本是把原来被测试的两个变量合并成一列,并在此基础上估计合并后事件A出现的概率。
对变量“是否丢失、是否有工作”进行双样本比例检验,设置的关注类别为1。具体的参数设置如下所示:
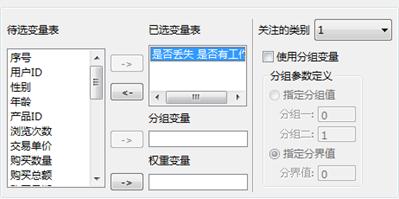
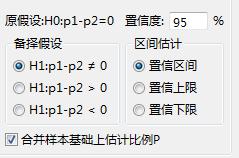 图 0-1 双样本比例检验-属性设置
图 0-1 双样本比例检验-属性设置
(2)输出结果
双击“运行”节点,得到计算结果如下:
 图 0-2 双样本比例检验-树形结果列表
图 0-2 双样本比例检验-树形结果列表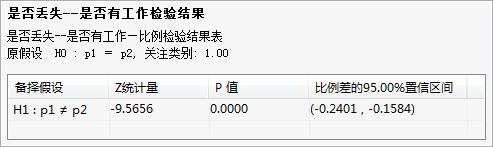 图 0-3 双样本比例检验-检验结果
图 0-3 双样本比例检验-检验结果
(3)结果说明
由P值为0.0000可知,P远小于0.05,则应拒绝原假设H0,认为p1≠p2。
输入变量变量表数据类型:二值数据、布尔型
输入分组变量数据类型:整型、浮点型、布尔型、字符型、日期型
输入数据尺度:标量型、名义型、有序型
有两个总体,它们分别含有某种性质的个体的比率为p1和p2,双样本比例检验依据来自这两个总体的独立样本,检验关于两总体比率是否有显著差异。
双样本比例检验是检验两个独立样本在n次独立重复试验中,其中一个样本序列和另外一个样本序列中事件A发生的频率大小的比较,即通过对样本进行二值概率检验,检验两个二值样本(0,1)中“1”出现的比例是否相等。
输出结果:
比例检验结果表:根据计算结果显示的显著性水平(p值)与设定的显著性水平(5%或其他)比较,若小于显著性水平则拒绝原假设;若大于显著性水平,则不能拒绝原假设。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1832****368 | 2019-01-21 09:42:54 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:48:09 | 1年 | Windows | 单机版 |
| 1840****220 | 2018-06-01 09:31:08 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-07 00:10:41 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-06 22:57:30 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:32 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:17 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:09 | 1年 | Windows | 单机版 |