
(1)设事件A在一次试验中发生的概率为p,记X为A状态,X=0为不发生,X=1为发生。进行n次独立重复试验,试对如下数据作p=0.5的双侧检验。以数据文件“马克威通用数据1.mkw”为例,演示单样本检验算法的操作。
首先,在工作区内,打开建模分析工作流:“基础分析→参数检验→单样本比例检验”,接着选择数据源,然后设置算法的参数,最后点击运行按钮。
其中各类参数的含义为:
变量表:一次可以选入一个或多个变量,变量必须为布尔型。
置信度:一般取95%,此时显著性水平α=0.05。
检验比例值:默认P=0.5。
备择假设:p≠p0是双尾检验,如果取显著性水平α=0.05,则拒绝区域为P值<0.025.而p>p0及p<p0是单侧检验,拒绝区域为P值<0.05。
区间估计:双侧置信区间的估计有两种方法:点估计法和解方程法。系统默认采用点估计法,用户可通过自定义来选择使用解方程法。
对变量“是否丢失”进行单样本比例检验,设置关注类别为1。具体的参数设置如下所示:
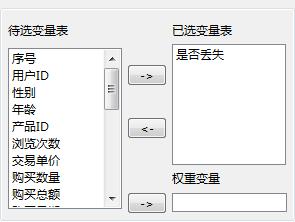
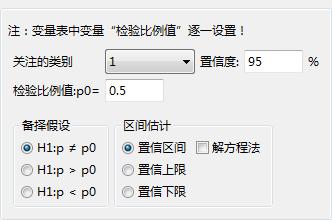 图 0-1 单样本比例检验-属性设置
图 0-1 单样本比例检验-属性设置
(2)输出结果
双击“运行”节点,输出分析结果:
 图 0-2 单样本比例检验-树形结果列表
图 0-2 单样本比例检验-树形结果列表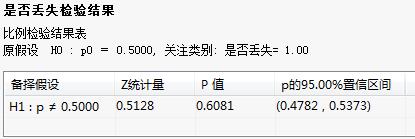 图 0-3 单样本比例检验-检验结果
图 0-3 单样本比例检验-检验结果
(3)结果说明
从计算的P值可以看出,P值远大于0.05,所以接受原假设,即是否丢失事件在一次试验中发生的概率等于0.5。
输入变量类型:整型、浮点型
输入数据尺度:标量型、名义型、有序型
单样本比例检验是检验在n次独立重复试验中,事件A出现的频率大小与给定频率之间是否存在显著性差异的统计分析方法。
单样本比例检验是检验关于比率的假设。假设总体中具有某种性质的个体的比率为p,根据来自总体的一个样本,检验比率p是否等于已知的某个常数。此检验适合于样本容量较大(一般≥30)的情形。
输出结果:
比例检验结果表:根据计算结果显示的显著性水平(p值)与设定的显著性水平(5%或其他)比较,若小于显著性水平则拒绝原假设。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1811****398 | 2018-07-23 13:52:02 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-07 00:10:41 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-06 22:57:30 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:40 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:35 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:33 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:28 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:27 | 1年 | Windows | 单机版 |