
(1)以数据文件“马克威通用数据1.mkw”为例,演示描述统计算法的操作。首先,在工作区内,打开建模分析工作流:“基础统计”→“描述统计”,接着选择数据源,然后设置算法的参数,最后点击运行按钮。
其中各类参数的含义为:
因子:用于选择分组变量,如果选择两个以上,系统会分别给出根据每个因子变量分组后的分析结果。因子变量可以为任意类型。
统计表:选择需要输出的统计结果:
描述:要求输出聚集态势表、离散态势表的有关指标量。
百分位数:反映变量取值分布情况的统计量。不同分位值之间的差距越大,表示数据在分布段上的离散程度越大。
极值:输出极限值表。
统计图:输出统计图,包括茎叶图和盒状图。
置信区间:默认值为95(%),必须设置为0~100之间的整数。
选择变量“购买总额”进行描述统计。具体的参数设置如下所示:
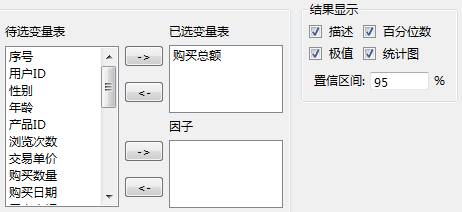 图 0-1 描述统计-属性设置
图 0-1 描述统计-属性设置
(2)输出结果
双击“运行”节点,输出分析结果:
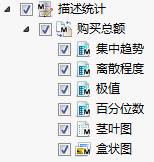 图 0-2 描述统计-树形结果列表
图 0-2 描述统计-树形结果列表 图 0-3 描述统计-集中趋势
图 0-3 描述统计-集中趋势 图 0-4 描述统计-离散程度
图 0-4 描述统计-离散程度 图 0-5 描述统计-极值
图 0-5 描述统计-极值
(3)结果说明
结果给出了“购买总额”的集中趋势、离散程度、极值等统计结果。集中趋势计算了均值、中位数、众数、最大值、最小值这些统计量;而离散程度计算了极差、方差、标准差、变异系数、偏度和峰度这些统计量。
输入变量类型:整型、浮点型
输入数据尺度:标量型、有序型、名义型
描述统计对数据进行分组统计分析,得出反映变量集中趋势、离散程度、异常值的各指标以及分位数表、茎叶图、盒状图。
描述统计是使用基本的“五值”统计量表现数据的集中度趋势,也可以根据事先设定的置信区间,得出置信区间内的上下限。该算法除了使用基本的统计指标如偏度、峰度、方差等来描述数据的离散程度外,还增加了茎叶图、盒状图来描述数据特征,使得结果更为直观。
百分位数:反映变量取值分布情况的统计量。不同分位值之间的差距越大,表示数据在分布段上的离散程度越大。
茎叶图:茎叶图主要有两列数,其中枝的跨度是指数据的级,即代表一个数据区间的长度,每隔一个级设置一个茎,相当于一个数据区间,每个茎下面有几个数就是几个叶。根据茎叶图中茎、叶的值,可以看出每个区间数据的分布情况。
盒状图:主要包含六个数据节点,将一组数按照从大到小排列,分别计算出上边缘值(最大值),上四分位数(75%分位数),中位数,下四分位数(25%分位数),下边缘值(最小值),以及异常值点。其中盒体部分主要是上下四分位数之间的数值,上下横线表示上下边缘值,散点表示异常值点。通过盒状图可以直观看到数据的中位数、尾长、异常值以及数据的集中度情况。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1305****178 | 2019-12-27 19:47:09 | 1年 | Windows | 单机版 |
| 1581****589 | 2019-04-02 14:29:40 | 1年 | Windows | 单机版 |
| 1393****839 | 2018-08-15 15:36:42 | 1年 | Windows | 单机版 |
| 1800****176 | 2018-08-15 15:28:57 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:52:02 | 1年 | Windows | 单机版 |
| 1840****220 | 2018-06-01 09:31:08 | 1年 | Windows | 单机版 |
| 1363****723 | 2018-03-08 16:54:38 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1368****837 | 2017-09-10 10:56:29 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |