
(1)以数据文件“马克威通用数据1.mkw”为例,选取前50条数据演示P-P图的操作。首先,在工作区内,打开建模分析工作流:“数据制图”→“P-P”,接着选择数据源,然后设置算法参数,最后双击运行按钮;其中各类参数的含义为:
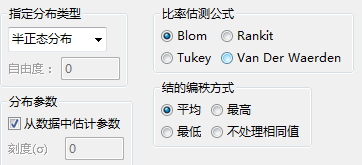
指定分布类型:用于指定待检验的分布,包括Beta分布、卡方分布、指数分布、Gamma分布、半正态分布、拉普拉斯分布、Logistic分布、对数正态分布、正态分布、Pareto分布、T分布、Weibull和均匀分布。针对某些分布需要设置自由度等必要参数。
分布参数:如果选中“从数据中估测参数”,则自动从数据中估测参数,并且输出参数,不选择该项,则可自行选择参数。
比率估测公式:提供了四种计算比例的方法,每次只能选择其中一项,以下公式中n是观测量的数目,r是从1至n的秩次。
Bloom:公式为(r-/3/8)/(n+1/4)
Rankit:公式为(r-1/2)/n
Tukey:公式为(r-1/3)/(n+1/3)
VarDerWaerden:公式为r/(n+1)
结的编秩方式:指定如何对结编秩。结指的是值相同观察数据。系统提供了以下四种对结的编秩方法:取平均、最高、最低和不处理相同值。
参数设置如下所示,变量选择“购买总额”:
(2)输出结果
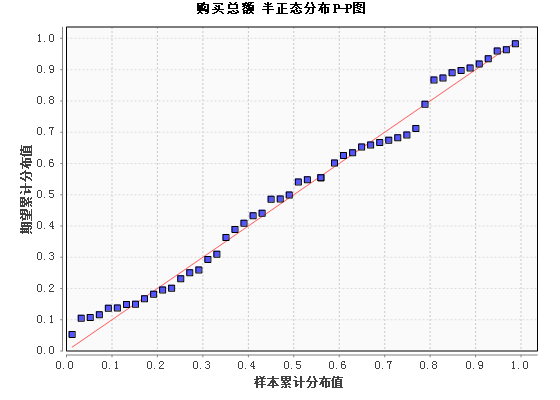
正态分布P-P图:
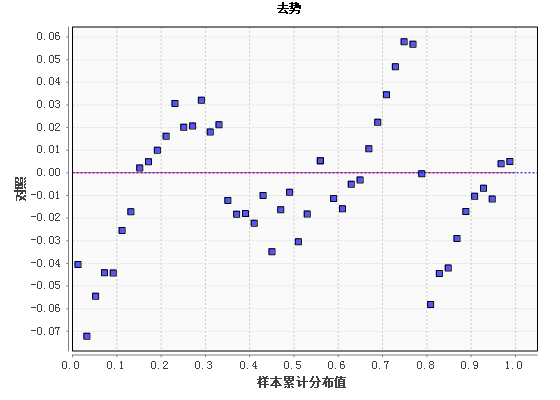
去势P-P图:
(3)结果说明
绘制数据的P-P图,如果数据服从某项分布,则图中数据点应和理论值(对角线)基本重合,在本例中,数据基本在一条直线上,即购买总额可认为是服从半正态分布的;
绘制数据的去势P-P图,反映的是按正态分布计算的理论值和实际值之差的分布情况,即分布的残差图,如果数据服从某项分布,则数据点应较均匀的分布在Y=0这条直线上下。图中可见残差正态评分的绝对值都在0.1以内,说明该数据符合半正态分布。
输入变量类型:数值型,如整型、浮点型、布尔型
P-P图是根据变量的累积概率对应于所指定的理论分布累积概率绘制的散点图,用于直观地检测样本数据是否符合某一概率分布。如果被检验的数据符合所指定的分布,则代表样本数据的点应基本落在代表理论分布的对角线上。
P-P图在绘制为比较两个概率分布所绘制的散点图时,首先要选择一系列采样点,对每个采样点分别计算其在两个分布上的累计概率函数值,作为画图点的坐标。
输出结果:
P-P图:给出P-P图,观测数据是否服从正态分布;
去势P-P图:给出理论值与实际值差值的分布情况。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1513****706 | 2021-07-05 16:18:43 | 1年 | Windows | 单机版 |
| 1305****178 | 2019-12-27 19:47:09 | 1年 | Windows | 单机版 |
| 1523****139 | 2019-03-04 22:52:36 | 1年 | Windows | 单机版 |
| 1840****220 | 2018-06-01 09:31:08 | 1年 | Windows | 单机版 |
| 1801****513 | 2018-04-07 13:53:02 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 12:17:53 | 1年 | Windows | 单机版 |
| 1340****082 | 2017-04-07 09:51:47 | 1年 | Windows | 单机版 |
| 1340****082 | 2017-04-07 09:51:47 | 1年 | Windows | 单机版 |
| 1340****082 | 2017-04-07 09:30:05 | 1年 | Windows | 单机版 |