
(1)以数据文件“二项分布.mkw”为例,演示二项分布检验算法的操作。数据为某地某时间内出生40名婴儿,其中女性12名(定性别=0),男性28名(定性别=1)。问这个地方出生婴儿的男女性比例与通常的男女性比例(总体概率约为0.5)是否不同?(性别:男性为1,女性为0)。
首先,在工作区内,打开建模分析工作流:“基础分析→非参数检验→二项分布检验”,接着选择数据源,然后设置算法中的参数,最后点击运行按钮。其中各类参数的含义如下:
变量表:系统支持的数据类型有:浮点型,整型,布尔型。
分界点:指定将序列分为两类的分界点。系统将小于等于分界点的所有值作为一组,将大于分界点的所有值分为另一组,然后计算个数。分界点指定包括不处理、平均值、中位数和用户指定四种方法。其中:
不处理:是指对序列不做任何处理,这种方法只适合于变量取值只有0和1两个数值的情况。
平均值:表示以样本平均值作为分界点,这种方法将大于样本平均值的数值归为一类,将小于等于样本平均值的数值归为一类。
中位数:表示以样本中位数作为分界点,这种方法将大于样本中位值的数值归为一类,将小于等于样本中位值的数值归为一类。
用户指定:表示以用户指定的点为分界点,这种方法将大于用户指定值的数值归为一类,将小于等于用户指定值的数值归为一类。
检验比率:指定检测概率。系统默认的检测概率是0.5,这意味要检测的序列是服从均匀分布的。如果每一项中个体的期望比率不等,则在右边的框中键入第一个值的概率期望值。
对于不处理的分界点:检验比率是指检验序列的第一个样本所对应的值出现的概率。
对于平均值的分界点:检验比率是指检验序列的第一个值所属于的组对应出现的概率。比如:序列的均值为85,序列的第一个值为80,则检验概率是指小于等于85的一组所出现的概率。
对于中位数的分界点:检验比率是指检验序列的第一个值所属于的组对应出现的概率。比如:序列的中位数为80,序列的第一个值为85,则检验概率是指大于80的一组所出现的概率。
对于用户指定的分界点:检验比率是指检验序列的第一个值所属于的组对应出现的概率。比如:用户指定分界点为80,序列的第一个值为85,则检验概率则是指大于80的一组所出现的概率。
设置好参数如下界面所示:
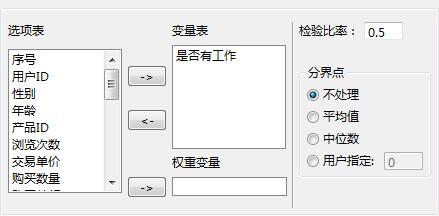
(2)输出结果
双击“运行”节点,系统进入分析过程,并输出结果如下所示:


(3)结果说明
二项分布检验表明:女婴12名,男婴28名,观察概率为0.70(即男婴占70%),检验概率为0.50,二项分布检验的结果是双侧概率为0.0166,可认为男女比例有显著差异,即与通常的0.5的性别比不同,该地男婴明显比女婴多。
输入变量变量表数据类型:整型、浮点型、布尔型
输入数据尺度:标量型、名义型、有序型
二项分布检验是用于检验一个观察序列是否满足二项分布 。根据样本数据推断总体的分布是否与指定的二项分布存在显著差异。
在样本数小于等于30时,按照计算二项分布概率的公式计算。在样本数大于30时,计算的是Z统计量,认为在零假设下,Z统计量近似服从正态分布。系统自动计算Z统计量并给出对应的相伴概率值。如果相伴概率值小于或等于给定的显著性水平 ,则拒绝零假设,即认为样本来自的总体与某个指定的二项分布有显著性差异。
检验结果:取值的实际频数、观察比率、检验概率和显著性水平。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1811****398 | 2018-07-23 13:48:09 | 1年 | Windows | 单机版 |
| 1840****220 | 2018-06-01 09:31:08 | 1年 | Windows | 单机版 |
| 1825****295 | 2017-09-15 10:07:26 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-07 00:10:41 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-06 22:57:30 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:39 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:31 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:20 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:17 | 1年 | Windows | 单机版 |