
(1)以数据文件“马克威通用数据1.mkw”为例,演示两个独立样本检验算法的操作。首先,在工作区内,打开建模分析工作流:“基础分析→非参数检验→两个独立样本检验”,接着选择数据源,然后设置算法中的参数,最后点击运行按钮。其中各类参数的含义如下:
分组变量:用来把参与运算的样本进行分类的变量。通过指定分组变量的取值,来确定变量的分类。两个独立样本检验要求指定分组变量的两个取值,把参与运算的变量分为两类。当然分组变量本身取值可以有多个类别,只有属于指定的分组取值的样本参与计算。
检验类型:选择检验的方法。
对变量“购买总额”进行两个独立样本检验,其分组变量为“是否有工作”。具体的参数设置如下所示:
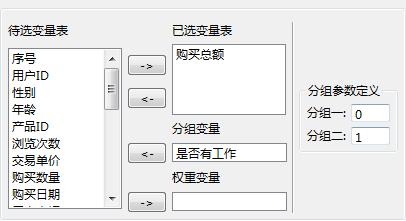
 图 0-1 两个独立样本检验-属性设置
图 0-1 两个独立样本检验-属性设置
选择变量“是否有工作”到分组变量栏,并设置不同的组值,双击“运行”节点,系统进入分析过程。
(2)输出结果
 图 0-2 两个独立样本检验-树形结果列表
图 0-2 两个独立样本检验-树形结果列表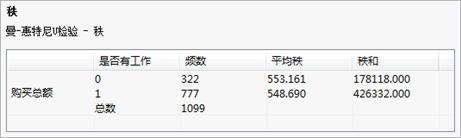 图 0-3 两个独立样本检验-秩-曼-惠特尼U检验
图 0-3 两个独立样本检验-秩-曼-惠特尼U检验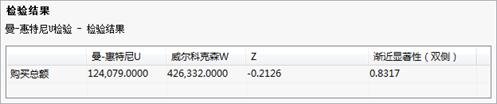 图 0-4 两个独立样本检验-曼-惠特尼U检验
图 0-4 两个独立样本检验-曼-惠特尼U检验
(3)结果说明
在第一张表中,两个样本的平均秩分别为553.161、548.69,说明两个样本的数据在整个数据中的位置和名次相差不大。
第二个表中P值(显著性)为0.8317>0.05,故接受原假设,可以认为两个独立样本的分布没有显著性的差异。
输入变量表数据类型:整型、浮点型、布尔型
输入数据尺度:标量型、名义型、有序型
两个独立样本的非参数检验是在对总体分布不甚了解的情况下,通过对两个独立样本的均值、中位数等进行差异检验,来分析它们是否来自相同的分布。独立样本是指在一个总体中随机抽样对在另一个总体中随机抽样没有影响的情况下所获得的样本。
系统提供了四种检验方法:曼-惠特尼U检验、沃尔德-沃尔佛威茨游程检验、柯尔莫哥洛夫-斯米尔诺夫检验和莫斯检验。
曼-惠特尼U检验
即两个独立样本的曼-惠特尼U检验(Mann-Whitney U),主要是通过对平均秩的研究来实现推断的。
沃尔德-沃尔佛威茨游程检验
即两个独立样本的游程检验(Wald-Wolfowitz Runs)。其基本思想与单样本游程检验的思想是相同的,不同点在于计算游程数的方法。在两个独立样本游程检验中,计算游程数的方法与变量的秩有关。如果样本来自的两个总体的分布形态存在较大的差距,那么计算出的游程数会相对较小。如果游程数比较大,则应该是由于两样本数据充分混合的结果,那么它们的分布应该不存在显著差异。
为作精确的判断,系统利用游程数构造计算Z统计量,并依据正态分布给出检验的P值。如果P值小于或等于给定的显著性水平,则拒绝零假设,认为样本来自的总体的分布存在显著性差异。
柯尔莫哥洛夫-斯米尔诺夫检验
即两个独立样本K-S检验(Kolmogorov-Smirnov Z)。其基本思想与单样本K-S检验的基本思路相同,差别在于这里处理的是变量值的秩,而非变量值本身。
两个独立样本K-S检验仍然关注差值序列,系统将自动计算K-S Z 统计量,并依据正态分布表给出检验的P值。如果P值小于或等于给定的显著性水平,则拒绝零假设,认为取得样本的两个独立总体的分布有显著差异。
莫斯检验
即两个独立样本的极端反应检验(Moses Extreme Reaction),是一种检验样本来自的两总体分布是否存在显著差异的检验。它将一个样本作为控制样本,另一个样本作为实验样本,以控制样本作为对照,检验实验样本是否存在极端反应。如果实验样本不存在极端反应,则认为两个独立总体分布无显著性差异。相反,如果实验样本存在极端反应,则认为两个总体分布存在显著差异。
首先,将两组样本混合并按升序排序;然后,找出控制样本最低秩和最高秩之间包含的观察个数,称为跨度。为控制极端值对分析结果的影响,也可先去掉控制样本两个最极端的变量值后再求跨度,这个跨度称为截头跨度。系统自动计算跨度和截头跨度后,会依据分布表给出对应的检验的P值。如果P值小于或等于给定的显著性水平,则拒绝零假设,认为样本来自的两个独立总体的分布存在显著差异。
输出结果:
检验结果:根据计算结果显示的显著性水平(p值)与设定的显著性水平(5%或其他)比较,若小于显著性水平则拒绝原假设,可以认为两个独立样本的分布存在显著性差异,否则表明不能拒绝原假设。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1811****398 | 2018-07-23 13:48:09 | 1年 | Windows | 单机版 |
| 1840****220 | 2018-06-01 09:31:08 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1832****368 | 2017-05-05 09:32:35 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-07 00:10:41 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-06 22:57:30 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:42 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:35 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:31 | 1年 | Windows | 单机版 |