
以数据文件“马克威通用数据3.mkw”为例,演示判别分析算法的操作。判别学生毕业之后是否找到工作与学历、期望薪酬、学校层次和家庭收入水平等变量之间的关系。
(1)首先,在工作区,打开建模分析工作流“高级统计”→“判别分析”;
(2)接着选择数据源;
(3)然后设置算法的参数;
(4)主要操作步骤如下:
1)选择数据源;
2)变量选择:
组变量:选择表明已知的观察量所属类别的变量(离散变量)。
自变量:选择表明观察量特征的变量。要求是数值型变量,如整型,浮点型,布尔型。
输出设置:选择要输出的判别分析结果。
选入/剔除标准:设置逐步法的选入、剔除标准。
设置好参数如下所示:
变量选择:
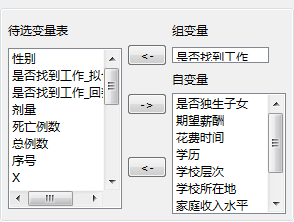
输出设置:

(5)输出结果:
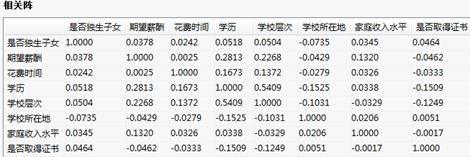
相关阵:
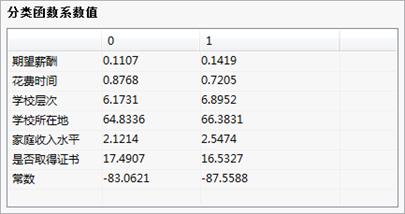
分类函数系数值:
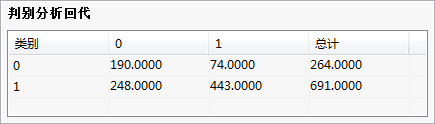
判别分析回代:
(6)结果说明:
相关阵表给出各变量之间的相关性大小;可以看出这个案例的8个变量的相关性还是挺小的;它们之间属于弱相关。
分类函数系数值给出判别函数的系数;即:各判别函数可如下表示:
F1 = -83.0621+17.4907*是否取得证书+2.1214*家庭收入水平+64.8336*学校所在地+6.1731*学校层次+0.8768*花费时间+0.1107*期望薪酬;
F2 = -87.5588+16.5327*是否取得证书+2.5474*家庭收入水平+66.3831*学校所在地+6.8952*学校层次+0.7205*花费时间+0.1419*期望薪酬;;
得到判别函数之后,可以将未知样品数据代入判别函数中,计算判别函数值,根据函数值可判别该样本属于第几类。
回代就是利用线性判别函数,对观测变量进行判别得出该观测量属于哪一类。对每一个观测量均使用该方法进行判别,然后统计错判率。
输入变量类型:要求数值型变量;如整型、浮点型、布尔型
注:输入变量中必须要有分组变量
输入数据尺度:标量型
判别分析是根据描述事物特征的变量值和它的所属类找出判别函数,并以此为依据对所研究事物进行所属类判别的一种方法。其目的是对已知分类的数据建立由数值指标构成的分类规则,然后把这样的分类规则应用到未知样本去分类。
判别分析广泛地应用于科学研究中,如:动植物分类,医学疾病诊断,社区种类划分,气象区域(或农业气象区)的划分,商品等级分类,职业能力分类,以及人类考古学中的年代归属及人种分类等等。
算法包含的各类基本统计量有:均值、离差及协方差。判别分析要求类别间的组内方差尽可能小,组间方差尽可能大;同时,特征值越大,区别已知类的能力越强。
算法的实现原理有:读入数据;计算统计量,包括:样本均值,总体均值,组内离差,总离差,组间相关阵等;判别分类:选择判别分类方法、计算判别系数、判别分类;判别效果检验。
计算判别系数:
(1)fisher’s法
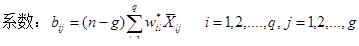
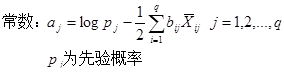
(2)距离判别法
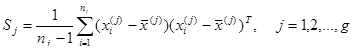
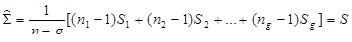
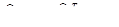
其中 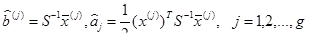
输出结果:
协方差表:给出不同分类变量的组内协方差值、总协方差值和变量的组间协方差值;
相关阵:给出变量之间的相关性大小;
F值和Lambad值:给出变量的F和Lambad值;
分类函数系数值:给出分类判别函数的系数;对未知数据可以带入分类函数,计算各函数值并取最大值,判别样本数据的分类结果;
判别分析回代、回代结果:给出判别分析的回代过程和结果;对观测量判别属于哪一类。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1832****368 | 2019-01-21 09:42:54 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:46:24 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1528****175 | 2017-06-15 14:23:53 | 1年 | Windows | 单机版 |
| 1803****455 | 2017-05-19 16:15:30 | 1年 | Windows | 单机版 |
| 1380****381 | 2017-04-08 01:04:27 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-07 00:10:41 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-06 22:57:30 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:40 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:22 | 1年 | Windows | 单机版 |