
以数据文件“马克威通用数据3.mkw”为例,演示主成分分析算法的操作。
(1)首先,在工作区,打开建模分析工作流“高级统计”→“主成分分析”;
(2)接着选择数据源;
(3)然后设置算法的参数;
(4)主要操作步骤如下:
1)选择数据源;
2)变量选择:
变量:参与主成分分析的变量,要求至少2个。系统支持整型,浮点型。
分析对象:选择分析的对象。
提取准则:选择因子的提取方法,并设置必要的参数。
主成分得分输出:输出主成分得分表格。
设置好参数如下所示:

(5)输出结果:
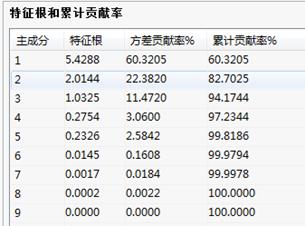
特征根和累计贡献率:
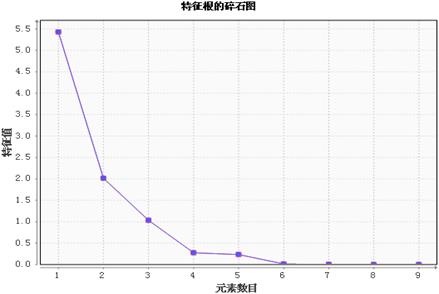
特征根的碎石图:
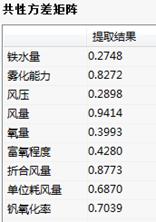
共性方差矩阵:
(6)结果说明:
特征根和累计贡献率表:因子列中表示因子的序号;特征根列中列出的是各主成分的特征值,特征根可以看成主成分影响力度的指标。表中列出了所有的主成分,它们按照特征根从大到小的次序排列。累计贡献率表示各因子的特征值占总方差的累计百分比。
特征根的碎石图给出了特征根的分布状况,从中可以直观地看出特征根的衰减情况以及每个特征根所作的贡献,用于决定保留多少个主成分。
共性方差矩阵表:反映的信息是按照所选标准提取相应数量主成分后,各变量中信息分别被提取的比例。
输入变量类型:要求数值型变量;如整型、浮点型
注:参与主成分分析的变量要求至少2个;数据要求没有缺损。
主成分分析构造原变量的一系列线性组合,使各线性组合在彼此不相关的前提下尽可能多地反映原变量的信息。
可应用于:概述数据之间的关系;将原数据转换为互不相关数据;降低数据个数,简化多变量维度;解决回归分析中共线性问题;可用来做一组变量的综合指数等。
可分析的对象:主成分分析可分析数据的不同统计量,系统支持对变量的相关系数和协方差进行分析。
可应用的领域:商业(如市场细分)、医学药理分析、化学分析、生物(如农作物生长的影响因素分析)、社会学、地质分析等。
主成分分析算法要求数据无缺损,所以将计算相关缺失值行都去除;输入数据矩阵,并赋予相应的权重;计算相关系数矩阵或协方差矩阵;计算数据矩阵的特征根和特征向量;选取特定的特征根和特征向量;计算因子载荷矩阵;计算数据矩阵的标准化得分;计算主成分。具体步骤如下:
1)计算相关系数矩阵和协方差矩阵:
叉积: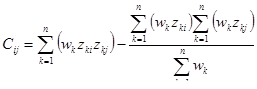 ,
,
相关系数矩阵: :
:
协方差矩阵: :
: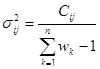
其中Z是数据,w是相应的权重。
2)计算相关系数矩阵或者协方差矩阵的特征根与特征向量:
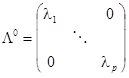 ,
,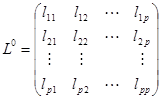
3)根据需求选取最大的前m个特征根与对应的特征向量:
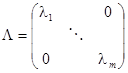 ,
,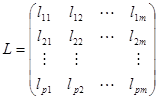
4)计算主成分贡献率及累计贡献率:
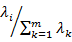 ,
,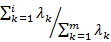
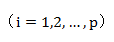
5)计算因子载荷矩阵和共性方差:
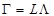 ,
,

6)计算数据矩阵的列进行标准化:
列均值: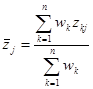 ,
,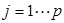
列方差: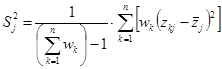 ,
,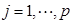
标准化元素: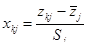 ,
, ,
,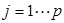
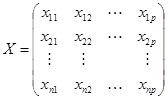
7)计算主成分:
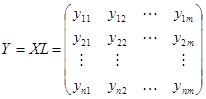
其中L为根据用户需求选取的特征根对应的特征向量。
输出结果:
主成分:表示采用主成分分析方法得到,每个主成分是原变量的线性组合,而每个主成分之间不相关;
特征根和累计贡献率:对矩阵相关系数进行特征值分解的结果,特征根越大对应因子的重要程度越大,用于确定公共因子的个数;
共性方差:反映了公共因子对原变量的影响或贡献率;
因子载荷矩阵:表明原变量与公共因子的相关系数;
反镜相协方差矩阵:原矩阵各变量的偏协方差矩阵取负号,反映了因子之间的相互关系;
反镜相相关系数矩阵:原矩阵各变量间偏相关系数矩阵取负号,代表了因子之间的相互解释程度;
再生相关系数(协方差):由因子载荷矩阵生成的相关系数,表示因子分析后因子的相关程度;
相关系数(协方差)残差:原矩阵相关系数和次生相关系数的差值;
巴特莱特球度检验:用于检验相关系数是否是单位矩阵,如果是单位矩阵就说明因子模型不适用。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1881****128 | 2024-08-16 16:53:03 | 1年 | Windows | 单机版 |
| 1590****469 | 2023-11-16 17:31:27 | 1年 | Windows | 单机版 |
| 1361****169 | 2019-04-01 17:24:26 | 1年 | Windows | 单机版 |
| 1805****256 | 2018-11-27 17:09:52 | 1年 | Windows | 单机版 |
| 1590****658 | 2018-09-09 21:17:27 | 1年 | Windows | 单机版 |
| 1786****104 | 2018-09-06 00:34:53 | 1年 | Windows | 单机版 |
| 1800****176 | 2018-08-17 10:12:15 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:46:24 | 1年 | Windows | 单机版 |
| 1830****649 | 2018-06-23 09:18:13 | 1年 | Windows | 单机版 |
| 1830****649 | 2018-06-23 09:16:18 | 1年 | Windows | 单机版 |