
以数据文件“马克威通用数据1.mkw”为例,演示单因素方差分析算法的操作。数据为顾客的喜好及购买商品总额,试分析不同爱好的顾客购买的商品总额是否有显著性的差异。
(1)首先,在工作区,打开建模分析工作流“高级统计”→“方差分析”→“单因素方差分析”;
(2)接着选择数据源;
(3)然后设置算法的参数;
(4)主要的操作步骤如下:
1)选择数据源;
2)变量选择:
变量表:选入需要分析的变量,如果选入多个结果变量(因变量),则
系统会依次对其进行方差分析。
因素:选入需要比较的分组因素,只能选入一个,建议分组变量为整
型,或者说具有真正分组意义的变量。
图表输出:选择结果的输出内容:
描述表:描述性分析表和方差分析表。
均值表:输出均值统计表。
直方图:用各组的均值做图,从该图中可看出均数间的大致趋势。
残差散点图:检验方差模型的有效性。
残差正态概率图:检验模型假设前提是否成立。
均值两两比较:选择进行方差齐性检验。
缺失值处理:选择缺失数据的处理方式:
仅去掉相关的行:与本次分析相关的变量中有缺失值的,则剔除该行。
去掉所有的行:只要记录中有缺失值的,不论缺失值所在变量是否
参与本次分析,均剔除该行。
设置参数好如下所示:


(5)输出结果:
购买总额描述分析:

购买总额巴特莱特检验:

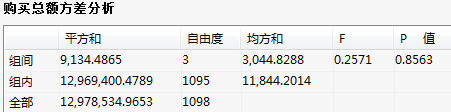
购买总额方差分析:
(6)结果说明:
购买总额描述分析表给出了购买总额的有效记录数、均值、标准误差、标准离差、自由度、置信区间等基本统计量;
购买总额巴特莱特检验得到显著性P值大于0.05,因此接受方差相等的假设,即分组数据方差相等;
购买总额方差分析表给出总观测变量的组间、组内平方和的大小;同时F检验的显著性水平P值远大于0.05,则认为分组数据的购买总额无显著性差异。
输入变量类型:要求数值型变量;
注:建议分组变量为整型。
单因素方差分析用来研究一个控制变量的不同水平是否对观测变量产生了显著性影响,还能用于两组及多样本均数的比较;可广泛应用于经济学、生物学、产品质量管理等各种分类过程中。
进行方差分析之后,有几个重要的分析要验证;1)需要检验控制变量的不同水平下观测变量总体方差是否相等进行验证,这是因为进行方差分析的前提是总体方差无显著性差异,无差异性即可认为总体的分布相同。2)想具体了解控制变量的水平对观测变量的影响程度,可以用多重比较检验;多重比较检验实现对各个水平下观测变量总体均值的逐渐比较。
方差分析主要是从质量因子的角度探讨因素的不同水平对实验指标影响的差异。一般来说,质量因子是可以人为控制的。
根据已有的计算公式,方差分析能够计算各类方差、误差、离差等统计量。设组数为k,第j组的例数为 ,
, ,离差平方和为SS,均方为MS,自由度为df,用b,e和t分别代表“组间”、“组内或误差”和“总合”。
,离差平方和为SS,均方为MS,自由度为df,用b,e和t分别代表“组间”、“组内或误差”和“总合”。
公式如下:
C(校正数)= ,
, ;
;
 ;
; ;
;
 ,
, ;
;
 ;
;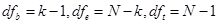
在计算结果中,观测变量的总离差平方和中,如果组间离差平方和所占比例较大,则说明观测变量的变动主要是由控制变量引起的,控制变量对其影响是显著的;反之,所占比例越小,则称控制变量的不同水平没有给观测变量带来显著性影响,观测值的变动是由随机因素引起的。
输出结果:
变量的描述分析:给出变量的有效记录数、均值、标准误差、标准利差、自由度、置信区间等基本统计量;
变量的方差分析:给出变量的组间、组内方差的平方和、自由度、均方和以及F、P值;
图形:给出变量的均值图、残差散点图、正态概率图和直方图等信息。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1832****368 | 2019-01-21 09:42:54 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:46:24 | 1年 | Windows | 单机版 |
| 1864****834 | 2018-07-23 11:37:39 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1300****148 | 2017-07-31 16:07:13 | 1年 | Windows | 单机版 |
| 1300****148 | 2017-07-31 16:05:52 | 1年 | Windows | 单机版 |
| 1550****026 | 2017-05-10 16:36:34 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-07 00:10:41 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-06 22:57:30 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:19 | 1年 | Windows | 单机版 |