
以数据文件“马克威通用数据3.mkw”为例,演示聚类分析算法的操作。
(1)首先,在工作区,打开建模分析工作流“高级统计”→“聚类分析”→“快速聚类”;
(2)接着选择数据源;
(3)然后设置算法的;
(4)主要步骤如下所示:
1)选择数据源;
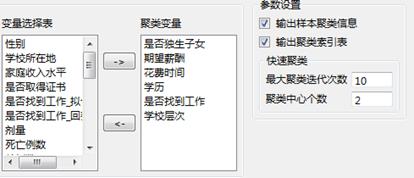
2)变量选择:
聚类变量:选入用于进行快速聚类的变量。参与快速聚类分析的变量必须是数值型变量且至少要有一个。
最大聚类迭代次数:设定最大迭代次数,默认值为10,当迭代次数等于指定的最大迭代次数时,迭代过程结束;迭代次数的范围在1~100000。
聚类中心个数:设置希望将样本分为的类别数,系统默认分为2类。聚类中心个数应该在2~1000的范围,且不能大于数据文件中的记录数。
3)指定需要输出的统计量。
样本聚类信息
聚类索引表
设置好参数如下所示:
(5)输出结果:
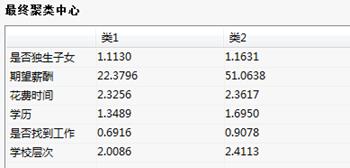
最终聚类中心:
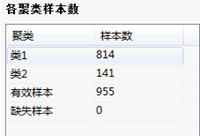
各聚类样本数:
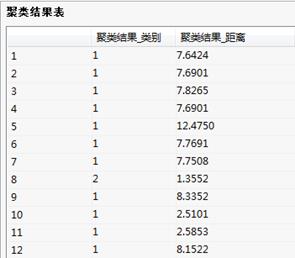
聚类结果表:
(6)结果说明:
最终表列出是最终聚类结果的聚类中心。聚类结果表列出的是聚类的详细结果。表中第一栏为选入进行快速聚类的变量各个观察记录的记录号。第二栏列出的是各样本数据点所属的类。第三栏为各样本数据点到本类中心点的距离。
输入变量类型:整型、浮点型、布尔型;
注:变量要求为连续型,各样本在d维空间中不能均匀分布,要能聚成类,并且各维要有相同的量纲;同时只能对记录进行聚类,而不能对变量聚类
输入数据尺度:标量型、名义型
快速聚类是聚类分析中使用较广的一种方法,它以距离来衡量样本间的远近程度,在聚类分析中,当样本量大于100时,有必要考虑快速聚类。因为快速聚类比分层聚类所需内存更少,计算速度更快。
快速聚类以距离衡量样本间的亲疏程度,但其最终结果不是聚成一类,而是根据各聚类中心,将所有样本点聚成指定的类数。
首先设置K个聚类的初始类中心点,计算所有样本点到K个类中心点的距离,按照距离最短的原则,将所有样本分派到各中心点所在的类中,形成一个新的K类,完成一次迭代过程。在下一次迭代过程中,重新计算K个类的类中心点,重复上述过程,直到达到指定的迭代次数或达到终止迭代的判断要求为止。
其中K个聚类初始中心点的选取有以下方法:
1)可以选取前K个观测变量值为初始中心点;
2)最小最大原则:先选择所有样本数据中距离最远的两个值;并且选择第三个值,使得与前两个聚点的距离最小者等于所有其余数据的较小距离中最大的,依次按这个原则选取,直到最终确定K个中心点;用公式可以表示为:
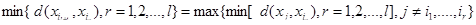
输出结果:
初始表:列出了各类初始聚类中心,初始聚类中心是系统根据样本数据的具体情况自动指定的。
最终表:列出是最终聚类结果的聚类中心。类的中心点表示类中所有变量的均值。
各聚类样本数表:列出各聚类各有多少个样本、总的有效样本、有没有缺失样本。
聚类结果表:列出的是聚类的详细结果。表中第一栏为选入进行快速聚类的变量各个观察记录的记录号。第二栏列出的是各样本数据点所属的类。第三栏为各样本数据点到本类中心点的距离。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1811****398 | 2018-07-23 13:46:24 | 1年 | Windows | 单机版 |
| 1853****355 | 2018-06-12 17:51:44 | 1年 | Windows | 单机版 |
| 1398****856 | 2018-01-04 02:06:08 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1314****646 | 2017-12-02 15:46:54 | 1年 | Windows | 单机版 |
| 1314****646 | 2017-12-02 15:46:36 | 1年 | Windows | 单机版 |
| 1886****205 | 2017-10-09 17:23:09 | 1年 | Windows | 单机版 |
| 1886****205 | 2017-10-09 17:22:32 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1894****057 | 2017-07-11 09:33:48 | 1年 | Windows | 单机版 |