
以数据文件“马克威通用数据2.mkw”为例,演示ARIMA模型算法的操作。这个算法能够用完成对变量x从序列平稳性到预测的全部分析。
(1)首先,在工作区,打开建模分析工作流“高级统计”→“时间序列” →“ARIMA模型”;
(2)接着选择数据源;
(3)然后设置算法的参数;
(4)主要操作步骤如下:
1)选择数据源;
2)变量选择:选择需要分析的变量到“已选变量”列表框;
3)指定模型参数:
自回归:指定自回归阶数p,要求为非负整数。
差分阶数:指定差分阶数d,要求为非负整数。计算自相关函数,使其很快衰减的d就是序列达到平稳的阶数。
移动平均:指定移动平均阶数q,要求为非负整数。(注:自回归阶数和移动平均阶数不能同时为零。)
带常数项:选择ARIMA模型是否包含常数项。
预测步数:即预测的步长,已知时间序列,预测后面的L个时刻的行为,则L即为预测的步数。
参数设置如下所示,自变量选择“x”,选择3阶自回归,预测步数为4:

(5)输出结果:
ARIMA模型参数估计:

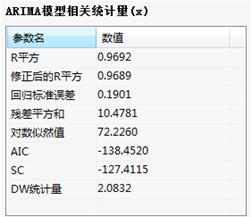
ARIMA模型相关统计量:
拟合图:

(6)结果说明:
输出结果这里主要给出了参数估计表、相关统计表、拟合图表。
ARIMA模型参数估计表中给出了自回归过程滞后3期的表达式,以及各个参数的t统计量和p值。
ARIMA模型相关统计量表中给出模型的拟合优度统计量,修正后的R平方、AIC值、DW值等。
拟合图可视化的给出了ARIMA模型的拟合状况。图中用绿色的线表示的即为预测数据。
输入变量类型:整型、浮点型
(注:参数选择要求为非负整数)
输入数据尺度:标量型
ARIMA模型又称自回归移动平均模型,是时间序列分析中最常用的模型之一;ARIMA模型对等间距时间序列进行观察、研究,找寻它变化发展的规律,预测它将来的走势;该模型是分析和预测等距序列数据、转移函数数据、干预数据的一种方法。
在经济预测中既考虑了经济现象在时间序列的依存性,同时考虑了随机波动的干扰性,对经济运行短期趋势的预测准确率较高,具有广泛的应用。
ARIMA模型通过其自身的过去值、过去误差、其他时间序列的当前值和过去值的线性组合来预测未来响应的时间序列。
该算法建模的基本要求是:要求序列的数列满足平稳条件,即个体值要围绕着均值上下波动,不能有明显的上升或下降趋势,如果出现较为剧烈的上升或下降趋势,应通过一次或多次差分,把一个非平稳的时间序列转换为一个平稳时间序列,将因变量Y对它的滞后值以及随机误差项的现值和滞后值进行回归,继而建立的模型。
ARIMA模型将预测指标随时间推移而形成的数据序列看作是一个随机序列,这组随机变量所具有的依存关系体现着原始数据在时间上的延续性,它既受外部因素的影响,又有自身变动规律。
输出结果:
ARIMA模型参数估计:输出参数检验的结果,如检验P值<0.05,说明对应的参数意义显著;
ARIMA模型相关统计量:给出模型的拟合优度统计量;如修正后的R平方越接近1,且与R平方越接近,说明模型拟合优度越高;
残差的白噪声检验:残差是预测值和真实观测值之间的差,此处检验残差是否为白噪声。
残差图:给出估计模型拟合的残差。
ARIMA模型拟合值:以图表的形式给出真实值和模型的拟合值以及预测值
拟合图:以图形的形式给出真实值和模型的拟合值以及预测值,从两条线的偏离程度我们可以估计模型的好坏,两条线越接近,则模型的拟和度越好,否则越差。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1881****128 | 2024-08-16 16:53:03 | 1年 | Windows | 单机版 |
| 1864****880 | 2023-06-20 00:35:48 | 1年 | Windows | 单机版 |
| 1580****863 | 2023-05-22 23:27:47 | 1年 | Windows | 单机版 |
| 1348****021 | 2022-11-19 21:27:22 | 1年 | Windows | 单机版 |
| 1348****021 | 2022-11-19 21:26:51 | 1年 | Windows | 单机版 |
| 1391****799 | 2019-03-31 13:50:15 | 1年 | Windows | 单机版 |
| 1864****834 | 2018-09-25 15:44:55 | 1年 | Windows | 单机版 |
| 1785****997 | 2018-06-17 12:26:33 | 1年 | Windows | 单机版 |
| 1362****882 | 2018-01-27 11:49:16 | 1年 | Windows | 单机版 |
| 1861****677 | 2018-01-20 09:43:10 | 1年 | Windows | 单机版 |