
以数据文件“马克威通用数据2.mkw”为例,演示单位根检验算法的操作。
(1)首先,在工作区,打开建模分析工作流“高级统计”→“协整分析”→“单位根检验”;
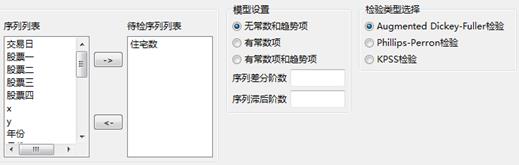
(2)接着选择数据源;
(3)然后设置算法的参数;
(4)主要的操作步骤如下:
1)选择数据源;
2)变量选择:
待检序列列表:选入要做单位根检验的变量。
模型设置:选择模型是否带常数项和/或趋势项,以及序列差分阶数和
序列滞后阶数。当检验类型为P-P检验或KPSS检验时,系统会将选项调整为“序列窗宽阶数”。
检验类型选择:选择检验的类型。
参数设置如下所示,待检验序列选择“住宅数”,差分阶数0阶,滞后阶数0阶:
(5)输出结果:
单位根检验统计量:

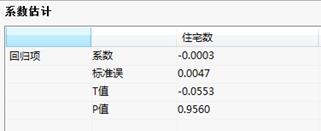
系数估计:
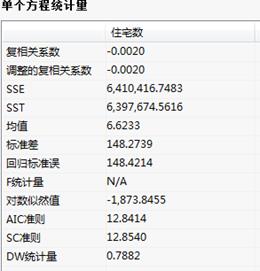
单个方程统计量:
(6)结果说明:
检验统计量表给出的是检验的统计量以及对应的不同水平的临界值。
系数估计表格给出的是对变量进行单位根检验生成的方程的系数,以及相应的系数标准误、显著性检验的T值和P值。
单个方程统计量表格给出的是针对变量的单位根检验生成的回归方程的显著性和相关统计量,其中AIC准则衡量方程的好坏,AIC准则越小方程越好。对于各变量的分析可采用不同方法检验,选择方程最好的进行预测、分类。
输入变量类型:要求数值型变量;如:整型、浮点型
单位根检验可用于对给定时间序列的平稳性进行检验,给出序列是否含有单位根;若不存在单位根,则检验的数据是平稳的;其中检验序列的平稳性对于序列识别和预测有重要意义,例如:若序列平稳,则可进行Granger因果检验,观察变量之间是否有某种因果关系;若不平稳,则可进行协整检验,检验变量之间是否存在长期的均衡关系;若考虑短周期波动影响,可用误差修正模型检验。
检验序列是否含有单位根;可用以下三种方法检验:
1)Augmented-Dickey-Fuller检验:当自回归包含滞后的变化时,基于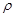 值、t检验或F检验的单位根检验称作扩大的迪基-富勒检验。即检验:
值、t检验或F检验的单位根检验称作扩大的迪基-富勒检验。即检验:
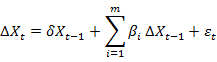
2)Phillips-Perron检验:P-P检验是基于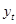 关于它的滞后值以及可能的常数项和时间趋势项的简单OLS回归。还可对标准OLS系数和t统计量做序列相关校正。检验方程:
关于它的滞后值以及可能的常数项和时间趋势项的简单OLS回归。还可对标准OLS系数和t统计量做序列相关校正。检验方程:
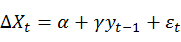 ,
,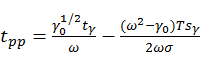
3)KPSS检验:Kwiatkowski-Phillips-Schmidt-Shin检验,从待检验序列剔出截距项和趋势项的序列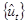 构造LM统计量。
构造LM统计量。
检验的参数说明:
1)若原序列中不存在单位根,则检验回归形式选择含有常数,意味着所检验的序列的均值不为0;若原序列中存在单位根,则检验回归形式选择含有常数,意味着所检验的序列具有线性趋势;
一个简单易行的办法是画出检验序列的曲线图,通过图形观察原序列是否在一个偏离 0 的位置随机变动或具有一个线性趋势,进而决定是否在检验时添加常数项。
2)若原序列中不存在单位根,则检验回归形式选择含有常数和趋势,意味着所检验的序列具有线性趋势;若原序列中存在单位根,则检验回归形式选择含有常数和趋势,意味着所检验的序列具有二次趋势。
同样,决定是否在检验中添加时间趋势项,也可以通过画出原序列的曲线图来观察。如果图形中大致显示了被检验序列的波动趋势呈非线性变化,那么便可以添加时间趋势项。
输出结果:
单位根检验统计量表:给出的是检验的统计量以及对应的不同水平的临界值。
系数估计表:给出的是对变量进行单位根检验生成的方程的系数,以及相应的系数标准误、显著性检验的T值和P值。
单个方程统计量表:给出的是针对变量的单位根检验生成的回归方程的显著性和相关统计量,其中AIC准则衡量方程的好坏,AIC准则越小方程越好。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1811****398 | 2018-07-23 13:44:40 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1528****175 | 2017-06-15 14:23:53 | 1年 | Windows | 单机版 |
| 1803****455 | 2017-05-19 16:24:39 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-07 00:10:41 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-06 22:57:30 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:37 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:24 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:02 | 1年 | Windows | 单机版 |