
以数据文件“马克威通用数据2.mkw”为例,演示协整检验算法的操作。
(1)首先,在工作区,打开建模分析工作流“高级统计”→“协整分析”→“协整检验”;
(2)接着选择数据源;
(3)然后设置算法的参数;
(4)主要的操作步骤如下:
1)选择数据源;
2)变量选择:
检验变量列表:待检验的变量。
外生变量列表:选入对要进行检验的变量有影响的变量,即外生变量,要求为浮点型变量。
滞后阶数:输入滞后阶数,要求为非负整数。
有无常数项和趋势:根据趋势项的性质,分为“无决定趋势”、“线性决定趋势”、“二次决定趋势”三大类,共五种模型。要求在其中选定一个,对常数项和趋势做出设定。
参数设置如下所示,检验变量列表:股票一、股票二,外生变量列表:股票四,参数设置选择滞后阶数为2阶:
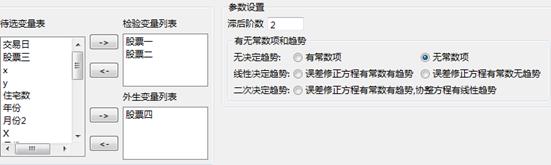
(5)输出结果:
轨迹检验:

最大特征值检验:

(6)结果说明:
输出结果主要有轨迹检验、最大特征值检验。
轨迹检验表给出协整关系的轨迹检验统计量,从结果可以看出两个变量是否有协整关系。
最大特征值检验表给出协整关系的最大特征值检验统计量,同上,也可以看出两变量是否有协整关系。
输入变量类型:要求数值型变量,如:整型、浮点型
协整检验分析检验变量间是否存在一种均衡关系;这种均衡关系可以表述为:在经济领域中,某些经济变量在某时期内受到干扰偏离长期的均衡点,在下一期调整以使其重新回到均衡状态。
协整检验分析可以应用于经济等领域的检验分析;也可用于检验非稳定的时间序列,观察他们是否有一定的线性组合使得该时间序列成为平稳序列。
协整检验的算法有:Johansen算法;该算法使用约束极大似然法进行检验;给出多个变量之间的协整关系,并且给出假设的协整模型的系数估计。Johansen检验要分为特征值轨迹检验和最大特征值检验。
其中两个变量的可用:Engle-Granger检验
第一步:用OLS估计方程: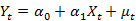 ;非均衡误差
;非均衡误差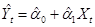 ,
, ;
;
第二步:检验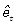 的单整性:
的单整性: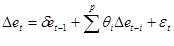 ;
;
多个变量可用扩展的E-G检验。
输出结果:
轨迹检验:给出协整分析的轨迹统计量;包括:特征值、检验统计量、不同临界值的值;
最大特征值检验:给出协整分析的最大特征值统计量;包括:特征值、检验统计量等;
协整系数估计:给出协整分析的变量的协整系数值;
分类系数估计:给出变量的分类系数值。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1521****939 | 2022-06-20 10:46:02 | 1年 | Windows | 单机版 |
| 1521****939 | 2022-03-02 17:52:51 | 1年 | Windows | 单机版 |
| 1865****010 | 2020-04-09 19:07:33 | 1年 | Windows | 单机版 |
| 1886****092 | 2018-09-02 10:13:17 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:44:40 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1825****295 | 2017-10-12 14:30:23 | 1年 | Windows | 单机版 |
| 1825****295 | 2017-10-12 14:27:23 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1528****175 | 2017-06-15 14:23:53 | 1年 | Windows | 单机版 |