
以数据文件“马克威通用数据2.mkw”为例,演示KM过程算法的操作。该文件是某研究者欲研究肺癌四种亚型的生存事件有无差别,收集了一些肺癌病例的数据;(变量说明:类型:即癌细胞病例类型。1=腺癌、2=大细胞癌、3=小细胞癌、4=鳞癌;生存时间:单位为天数;健康指数:为病人入院时的身体健康指数,取值在0~100之间;时间间隔:为从诊断为肺癌到开始治疗的时间间隔(月);年龄:病人的年龄;性别:1=男性,2=女性;生存状态:0=失访,1=死亡。)本例要求比较四种病例类型肺癌病人的生存率。
(1)首先,在工作区,打开建模分析工作流“高级统计”→“生存分析”→“KM过程”;
(2)接着选择数据源;
(3)设置算法的参数;
(4)主要操作步骤如下:
1)选择数据源;
2)变量选择:
时间变量:用于选入生存时间变量,变量中不能有负数。
状态:用于选入生存状态变量。该变量用来标定删失和非删失状态。在
选入生存状态变量后,设置事件发生的数值:
值:单变量用于在状态变量中选择某个变量值,系统只对该变量值的生存时间进行分析,其他未选变量值的生存时间按删失值处理。例如,在状态变量中有0、1、2、3四种变量值,如果在该框中键入“2”,只对状态2的生存时间分析,而忽略其他三种变量值的生存时间分析。
范围:在状态变量中选择一个变量值范围,系统只对该变量值的生存时间进行分析,其他未选变量值的生存时间按删失值处理。例如,在状态变量中有0、1、2、3四种变量值,如果在该框中键入“1”和“3”,只分析状态1、2、3的生存时间,而忽略状态0的生存时间分析。
因素:用于定义进行比较的研究因素。
参数设置如下所示,分析的变量分别为数据表中的“生存时间”、“生存状态”、“类型”:

(5)输出结果:
各因素类型表:
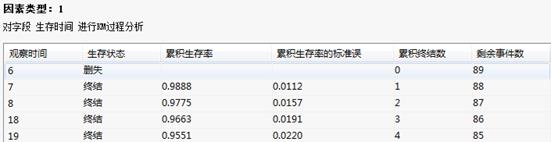





汇总统计表:

(5)结果说明:
分析结果给出了各因素统计表,汇总统计表。
因素统计表给出了观察时间、生存状态、累计生存率、剩余事件数等统计量,汇总统计表分四种肺癌类型的汇总:分别输出了各组患者数、删失值数及其所占的比例。
输入变量类型:整型
注:数据集合;要求输入时间变量;输入状态变量,包括终结事件定义(单值或范围值);有因子字段(分组)
输入数据尺度:标量型,名义型
Kaplan-Meier称乘积极限估计,可以对一个影响因素进行检验;本方法适用于以个体为单位来收集信息的未分组生存数据,分析重点是计算每一“结果”事件发生时点的生存率。
用于样本含量较小情形,不能给出特定时间点的生存率。可应用领域为:产品质量检验、药品疗效检验、金融保险业和人群寿命统计等。
KM估计生存曲线:首先计算出活过一定时期的病人再活过下一时期的概率(即生存概率),然后将逐个生存概率相乘,得到相应时段的生存率。KM算法计算案例出现观察终点时的生存概率,计算结果更精确。
KM算法模型中包含的变量有:某一组案例总数目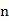 ;观察时间;生存状态;累积生存率。
;观察时间;生存状态;累积生存率。
某一组的案例总数目为n,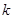 为观察时间点数目,
为观察时间点数目,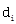 为第
为第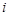 个时间点的失效事件数目,
个时间点的失效事件数目, 为第
为第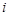 个时间点的观察案例数目,
个时间点的观察案例数目,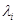 为第
为第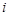 个时间点的删失事件数目。
个时间点的删失事件数目。
 ,
, 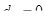 ,
, ,
,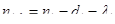 ;
;
则累积生存率为
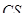 =
=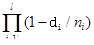 ,
, ,如果
,如果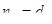 ,则
,则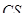 =0;
=0;
累积生存率的标准误:SECSl=CSl ,
, ;
;
累积失效事件数目: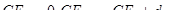 ;
;
相应时间的剩余数目: ;
;
平均生存时间:Mean=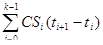 ;
;
中位生存时间:终结事件数达到输入数据一半的时间。
输出结果:
每种类型的生存分析表:包含观察时间、生存状态、累积生存率、累积生存率的标准误差、累计终结数、剩余数目、平均生存时间、中位生存时间等;
汇总表:总数、事件数目、失访事件数目、失访事件百分比等。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1832****368 | 2019-01-21 15:51:48 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:44:40 | 1年 | Windows | 单机版 |
| 1565****880 | 2018-06-02 11:02:00 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1825****295 | 2017-09-06 17:01:10 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1528****175 | 2017-06-15 14:23:53 | 1年 | Windows | 单机版 |
| 1376****104 | 2017-05-04 11:53:58 | 1年 | Windows | 单机版 |
| 1832****698 | 2017-04-11 09:33:05 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-07 00:10:41 | 1年 | Windows | 单机版 |