
以数据文件“马克威通用数据1.mkw”为例,演示广义回归算法的操作说明。该算例只研究模型的系数评估和模型的求解过程;其他,如模型系数检验、模型残差检验和模型稳定性检验等内容,可自行操作理解。
在工作区,打开建模分析工作流“高级统计”→“回归分析”→“广义回归”,接着选择数据源,然后设置算法的参数。具体步骤如下:
1. 选择数据源;
2. 输入方式选择:选择 “选择变量”列表框;
3. 选择分析变量:将要分析的变量分别选入列表框;
4. 选择要分析显示的结果;
5. 点击运行节点。
(1)选择变量参数
选择“系数估计”功能;其中各参数变量的说明如下:
方程描述:用公式定义方程,只需在对话框中输入表达式;
估计方法:
最小二乘法:模型满足古典假设时估计出的系数是无偏的有效的。
两阶段最小二乘法:解释变量与扰动项相关时,找到一组与扰动项不相关的工具变量。
区间变量:用户指定作为区间变量,必须为连续的日期型序列;
估计区间:输入开始时间和终止时间;
异方差自相关一致协方差:处理模型存在自相关和异方差;
权重设置:当方程存在异方差且已知时,可以输入权重的表达式;
模型保存路径:将估计完成的带有系数的模型保存用作预测。
参数设置如下所示:
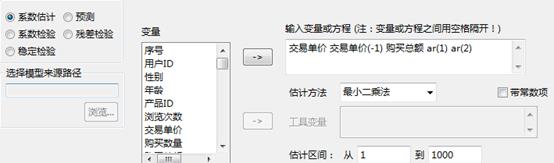
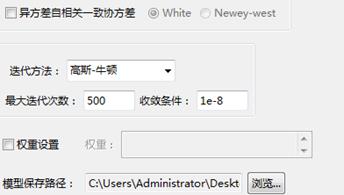
(2)输出结果:
方程

参数估计:

相关统计表:

(3)结果说明:
输出结果中给出了回归方程,参数估计表中给出了各个参数的估计量以及误差、t值、P值,方便查看系数的显著性。相关统计量表中给出了R平方、修正R平方、回归标准误差等统计量的数值,根据这些指标可以判断模型的情况。
(4)选择“预测”选项,界面切换到预测设置,到“系数估计”时模型的保存路径下打开模型,其中各参数的说明如下:
模型来源:选择系数估计时所建的模型;
预测方法:包含静态预测和动态预测两种方法。
动态预测:进行预测时只使用求解样本期之前的内生变量。滞后内生变量和ARMA项是利用前几期的解计算的,而不是来自实际的历史数据。
静态预测:每次求解模型时直到前一期的内生变量都被使用。滞后内生变量和ARMA项取自内生变量的实际值。
忽略AR项:当方程中含有AR项时,此选项有效,勾选后再预测时方程中的AR项不参与求解。
预测区间:因变量求解的区间。
参数设置如下所示:

(5)输出结果:
预测值表:
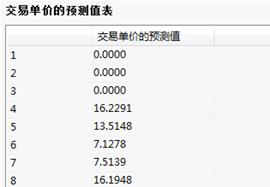
(6)结果说明:
交易单价的预测值表中给出了交易单价的预测值,这里只截取了前8个。
输入变量类型:整型、浮点型
输入数据尺度:标量型
广义回归可以应用于经济学数据的预测处理;经济计量研究始于经济学中的理论假设,根据经济理论设定变量间的一组关系,如消费理论、生产理论和各种宏观经济理论;对理论设定的关系进行定量刻画,如消费函数中的边际消费倾向、生产函数中的各种弹性等进行实证研究。
广义线型回归是指参数线型回归(即参数仅以一次方的形式出现在模型中),而解释变量并不一定是线性的。广义线性回归模型的自变量可以是离散的,也可以是连续的;离散的取值可以为二值的,也可为多值的。同时广义回归的随机误差项不一定服从正态分布,可以是其它的指数分布族;如二项、泊松、负二项伽马等分布。
广义回归模型的建立包含三个部分:选择变量、确定变量之间的数学关系、拟定回归方程中需要估计的参数的数值范围。确定模型中所包含的变量主要是指确定解释变量(因变量);确定模型的数学形式主要是选择适当的数学形式描述变量之间的关系,当事先无法确定模型的数学形式时,可以采用各种可能的形式进行试模拟,选取结果较好的一种数学表达式形式;拟定理论模型中需要估计参数的范围可以用来检验模型的估计结果。
输出结果:
模型说明:给出模型数据的来源,记录数等信息;
方程:给出自变量与因变量的回归方程;
参数估计:估计自变量的系数;
相关统计量:给出各类统计量,如:R平方、修正后的R平方、回归标准误差、残差平方和等统计量;其中根据R和修正R平方值的大小,判断回归方程的准确性,值越大,说明拟合的准确性越好;
残差表:给出实际数据与回归数据的残差;
预测值表:给出训练得到的回归方程计算得到的结果值;
预测值图:给出预测值的图形表示结果,能直观的看出预测结果的准确性。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1381****445 | 2022-03-07 13:36:28 | 1年 | Windows | 单机版 |
| 1371****011 | 2020-09-30 21:22:13 | 1年 | Windows | 单机版 |
| 1851****627 | 2018-11-07 12:28:23 | 1年 | Windows | 单机版 |
| 1886****092 | 2018-09-02 10:13:17 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:48:09 | 1年 | Windows | 单机版 |
| 1381****880 | 2018-04-27 04:32:01 | 1年 | Windows | 单机版 |
| 1362****882 | 2018-01-28 19:46:34 | 1年 | Windows | 单机版 |
| 1362****882 | 2018-01-27 11:49:16 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |