
(1)以数据文件“马克威通用数据1.mkw”为例,演示期望最大化(EM)算法的操作。首先,在工作区内,打开建模分析工作流:“机器学习”→“EM”,接着选择数据源,然后设置算法的参数,最后点击运行按钮。
其中各类参数的含义为:
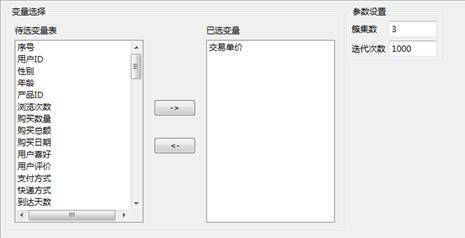
簇集数:聚类中心的个数
迭代次数:最大迭代次数
设置好参数如下所示:
(2)输出结果

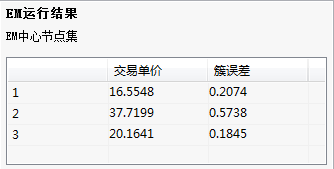
(3)结果说明
给出交易单价三个聚类中心。
输入变量类型:数值型数据
期望极大化(Expectation Maximization,EM)算法是一种解决含有隐含变量优化问题的有效方法,常用在机器学习和计算机视觉的数据聚类,高斯混合模型的参数估计。
EM算法已经在实际领域中得到广泛的应用,包括市场研究、模式识别、数据分析和图像处理。在商务中,可以用来发现不同的顾客群,刻画顾客的特征;在生物学中,能够用来推到动植物分类等。
EM算法是一种迭代算法,用于含有隐变量的概率模型参数的极大似然估计,或极大后验概率估计。当给定样本观测变量数据为X,隐变量数据为Z,联合分布表示为p(X,Z|θ),条件分布可以表示为p(Z|X,θ))。那么,估计模型的形式可以表示为:
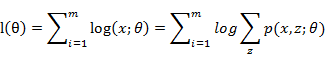
由于模型中存在隐含变量,并不能直接采用极大似然估计法,或贝叶斯估计法估计上述模型的参数。EM算法能够通过不断求解下界的极大化逼近求解对数似然函数,如图所示
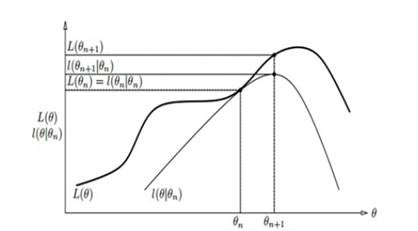
EM算法的每次迭代包含两步:
EM算法-E步:利用对隐藏变量的现有估计值,计算其最大似然估计值,以此实现期望化的过程,即:
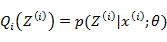
EM算法-M步:最大化在E步上的最大似然估计值来计算参数的值,每次迭代使得似然函数增大或达到局部极值,即:
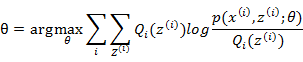
EM算法的最大优点是简单性和普适性。EM算法对于初值的选择非常重要,常用的方法是选取几个不同的初值进行迭代,然后比较得到的估计值,选取最优的。EM算法采用下界迭代的方法,这样并不能保证找到全局最优解。
输出结果:
给出聚类中心及簇误差。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1786****815 | 2023-03-10 14:12:48 | 1年 | Windows | 单机版 |
| 1864****834 | 2021-01-26 12:28:18 | 1年 | Windows | 单机版 |
| 1561****042 | 2019-05-28 23:41:00 | 1年 | Windows | 单机版 |
| 1361****169 | 2019-04-01 17:30:32 | 1年 | Windows | 单机版 |
| 1801****427 | 2019-02-18 19:07:33 | 1年 | Windows | 单机版 |
| 1570****389 | 2018-12-31 18:19:00 | 1年 | Windows | 单机版 |
| 1821****360 | 2018-10-13 14:17:58 | 1年 | Windows | 单机版 |
| 1864****834 | 2018-09-25 15:47:28 | 1年 | Windows | 单机版 |
| 1827****545 | 2018-09-16 08:55:41 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:11:06 | 1年 | Windows | 单机版 |