
选择数据文件为“马克威通用数据3.mkw”,演示聚类分析的操作。(注:因本例中两变量的量纲一样,所以可以不进行数据的标准化转换。)
(1) 首先,在工作区,打开建模分析工作流“高级统计”→“聚类分析”→“分层聚类”;
(2) 接着选择数据源;
(3) 然后设置模型参数;
(4) 具体操作如下。
1) 变量选择:
聚类变量:选择聚类的变量。
聚类对象与方法:指定聚类的对象是针对样本还是变量。同时,选择聚类的方法。选择“样本”是以每一行记录作为分析对象,选择“变量”为对每列变量作为分析对象。
测度方法:选择聚类时距离参数的测度方法,并设置必要的参数。
数据转换与输出图:选择系数的标准化方法,并指定输出图。
聚类个数:指定分层聚类的聚类数目。
输出各类索引表:指定输出聚类索引表。
参数设置如下,聚类变量为“是否独生子女”、“期望薪酬”、“花费时间”、“学历”、“是否找到工作、“学习层次”。聚类方法为组间连接法,测量方法为欧氏聚类,聚类个数为2,数据转换与输出图为Z分数方法,同时输出谱系图:
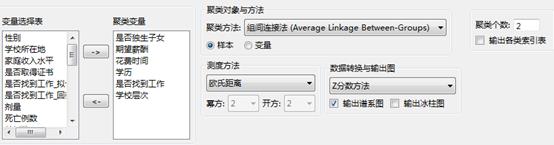
(5)输出结果:
聚类步骤表:
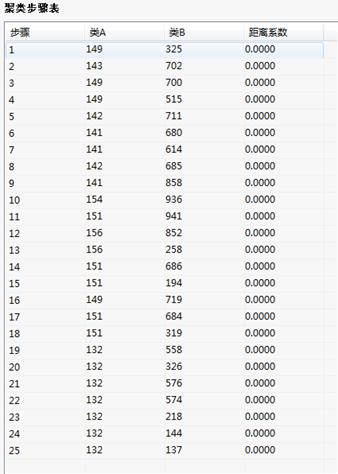
谱系图:
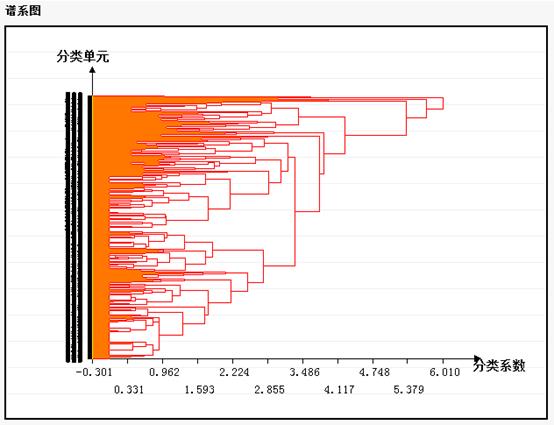
(6)结果说明:
聚类步骤表所列的是聚类过程的各步骤,第一栏列出的是聚类步骤序号,第二、三栏列出了合并的两类的序号,最后一栏“系数”栏列出的是合并的两类的系数。由聚类分析的原理可知,个案之间亲密程度最高的,即距离最小或相似系数最接近1或-1的最先合并。不同的聚类方法和测度方法以及是否进行数据转化,系数值会完全不同。
冰柱图给出了不同聚类数的分类规则,谱系图就是聚类步骤表的图形表示。
输入变量类型:整型、浮点型、布尔型等,无特殊数据要求
(注:聚类变量必须是数字型字段)
输入数据尺度:标量型、名义型、有序型
分层聚类是聚类分析的一种方法,聚类分析的目的就是把相似的东西归为类,减少差异。分层聚类适用于样本量较少的分析场景。
应用领域为:自然科学研究、社会科学研究、工农业生产等。
开始时将N个观测量(变量)视为N类;规定相似性统计量的测度,并计算相似系数矩阵;
找出最大相似系数的观测量(变量)组: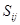 为类
为类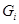 与类
与类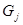 的相似系数,
的相似系数,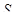 为相似系数矩阵或不相似系数矩阵,若
为相似系数矩阵或不相似系数矩阵,若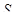 为相似系数矩阵,则依据
为相似系数矩阵,则依据 最小者挑选
最小者挑选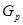 与
与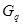 (
(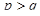 ),若
),若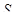 为不相似系数(距离)矩阵,则则依据
为不相似系数(距离)矩阵,则则依据 最大者挑选
最大者挑选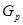 与
与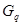 进行聚类,即将
进行聚类,即将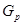 与
与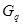 合并成一个新类
合并成一个新类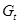 (
(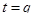 );
);
计算新类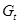 与当前各类的相似性系数,更新相似系数矩阵
与当前各类的相似性系数,更新相似系数矩阵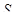 :将得到的新的系数代换与
:将得到的新的系数代换与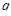 相关的行与列,删除与
相关的行与列,删除与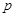 有关的行与列;
有关的行与列;
重复过程:寻找最大相似系数观测变量组和计算相似系数矩阵,直至聚为一类;
系统共提供了六种分层聚类的方法,五种距离尺度标准。如:明考斯基距离、马氏距离、匹配距离等。
输出结果:
聚类步骤表:聚类步骤表所列的是聚类过程的各步骤,第一栏列出的是聚类步骤序号,第二、三栏列出了合并的两类的序号,最后一栏“系数”栏列出的是合并的两类的系数。
谱系图:表明每一步中被合并的类及系数值。
冰柱图:把聚类信息综合到一张图上。系统所输出的冰柱图为纵向冰柱图,参与聚类的个体各占一列,标注个体号或在图纸允许的情况下标注个体的标签。聚类过程中的每一步占一行,标注每步的顺序号。冰柱图用于显示各变量依次在不同类别数时的分类归属情况。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1772****131 | 2023-12-12 13:54:51 | 1年 | Windows | 单机版 |
| 1590****469 | 2023-11-16 17:34:28 | 1年 | Windows | 单机版 |
| 1399****246 | 2020-01-20 16:56:12 | 1年 | Windows | 单机版 |
| 1832****368 | 2019-01-21 15:51:48 | 1年 | Windows | 单机版 |
| 1786****104 | 2018-09-06 00:34:53 | 1年 | Windows | 单机版 |
| 1886****092 | 2018-09-02 10:13:17 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:14:11 | 1年 | Windows | 单机版 |
| 1853****355 | 2018-06-12 17:11:47 | 1年 | Windows | 单机版 |
| 1302****267 | 2018-01-09 09:38:57 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |