
以数据文件“马克威通用数据2.mkw”为例,演示季节解构算法的操作。数据记录的是某市商品房从1979年到2002年月销售量的数据,试用季节解构模型完成从序列平稳性到预测的全部分析。
(1)首先,在工作区,打开建模分析工作流 “高级统计”→“时间序列” →“季节解构模型”;
(2)接着选择数据源;
(3)然后设置算法的参数;
(4)主要操作步骤如下:
1. 选择数据源;
2. 变量选择:
已选变量:选入进入分析的序列变量。
周期:可选择3~12之间的任意整数。一般选择4或12,若选择4,则分析四季对序列的影响;选择12,则分析月度对序列的影响。
预测步数:应输入不小于0的整数。
方法:包括乘法模型和加法模型两种。模型的选择要根据季节因素和线性因素的作用方式而定。
设置好参数如下所示:

(5)输出结果:
季节因子:
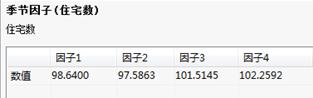
其他因素:

季节解构模型预测值(住宅数):
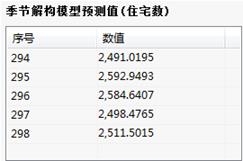
(6)结果说明:
分析结果给出了季节因子表、其他因素表、预测值表。
季节因子表给出所分析的序列受四个季节影响的相对比重。由于在参数选项中选择了“周期”数为4,所以4个因子分别为春夏秋冬4个季节因子。根据表中数据提示冬季对销售量的影响最大,夏季对销售量的影响最小。
其他因素表中第一列为数据文件的记录号。其余各列为根据原序列生成的移动平均序列、季节-不规则成分、调整后的季节序列、平滑趋势-循环序列和不规则成分5个序列。
对以上的5个序列分别画出序列图。季节解构模型预测值给出模型预测的住宅数。
输入变量类型:整型、浮点型;
(注:具有周期性质的序列,并要求序列有相应的年、月、日,不处理数据有缺失情况。)
输入数据尺度:标量型,有序型。
季节解构模型一般用于季节型时间序列分析,它将时间序列的信息分解如下四种信息:线性趋势、季节变化、循环变化和不规则四大因素。这四种信息与原时间序列的关系可以通过乘法模型和加法模型两种形式组合。
通过模型分析,可将原序列分解为长期趋势,季节因素和不规则因素等。季节结构的过程:
通过移动平均法使序列平滑—反映“趋势-循环”因素;除以(减去)平滑后的值—得到“季节—不规则”因素;将“季节”因素从“季节—不规则”因素分离出来。
建模的方法包括:乘法模型和加法模型。
乘法模型: 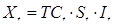
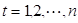
加法模型: 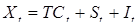
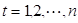
其中, 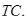 为“趋势-循环”因素;
为“趋势-循环”因素;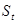 为“季节”因素;
为“季节”因素;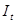 为“不规则”因素。模型的选择要根据季节因素和线性因素的作用方式而定。
为“不规则”因素。模型的选择要根据季节因素和线性因素的作用方式而定。
输出结果:
季节因子表:给出所分析的序列受四季节影响的相对比重。因子1到因子4分别代表春、夏、秋、冬。若周期为12,则季节因子表将输出因子1到因子12的相对比重,12个因子分别代表12个月份。
其他因素表:也为季节分析表,第一列为数据文件的记录号。其余各列为根据原序列生成的移动平均序列、季节-不规则成分、调整后的季节序列、平滑趋势-循环序列和不规则成分5个序列。
季节解构模型预测值:给出模型预测的数值。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1731****310 | 2020-01-19 14:19:33 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1528****175 | 2017-06-15 14:23:53 | 1年 | Windows | 单机版 |
| 1398****133 | 2017-05-12 12:11:42 | 1年 | Windows | 单机版 |
| 1805****709 | 2017-04-21 20:42:03 | 1年 | Windows | 单机版 |
| 1805****709 | 2017-04-21 20:30:47 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-07 00:10:41 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-06 22:57:30 | 1年 | Windows | 单机版 |
| 1382****701 | 2017-04-02 11:34:42 | 1年 | Windows | 单机版 |