
以数据文件“马克威通用数据1.mkw”为例,演示主成分回归算法的操作。该数据表示:有人在某地抽样调查了29例儿童的血红蛋白与4中微量元素的含量,问:可否用4中微量元素钙(X1)、镁(X2)、铁(X3)、铜(X4)来较好的预测血红蛋白的某个指标(Y)的含量。
(1)首先,在工作区,打开建模分析工作流,选择“高级统计”→“回归分析”→“主成分回归”;
(2)接着选择数据源;
(3)然后设置算法的参数;
(4)下面给出操作步骤:
1)选择数据源;
2)变量选择:选择需要分析的被解释变量到“因变量”列表框;解释变量到“自变量”列表框;
3)指定模型参数:
主成分选取原则:选择主成分的选取方法(原则),并设置必要的参数。
自定义主成分数:用户自定义主成分数,默认为2;
累计贡献率法:即累计贡献率不低于某个值,默认为80%;
对应特征值不太小法:此方法认为主成分对应特征值不应太小,默认为取特征值≥0.01;
缺失值处理:选择缺失值的处理方式。
参数设置:对模型的常数和输出进行必要的设置。
参数设置如下所示,因变量为“血红蛋白”,自变量为“钙”、“镁”、“铁”、“铜”,参数设置选择“累计贡献率不低于0.8”:

(5)输出结果:
主轴(对应主成分)信息表:

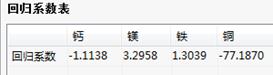
回归系数表:
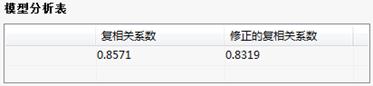
模型分析表:
回归方程:

(6)结果说明:
主轴(对应主成分)信息表给出各个主成份对应的统计量和组成,从中我们可以看出第一主成份所占的贡献率为62.1938%,第一、二主成份所占的累计贡献率为83.8573%。
回归系数表给出模型的回归系数列表,得到选取第一、二个主成份得到的回归方程。
模型分析表给出了最终模型的检验,最后给出了的回归方程。
输入变量类型:整型、浮点型,数据要求没有缺损。
输入数据尺度:标量型
将主成分分析用在多元线性回归中,便产生了主成分回归。当线性回归模型自变量间存在多重共线性时,主成分回归在不损失大量信息的前提下,降低分析变量的维度,将原来的多个指标组合成少数几个指标,新的指标之间相互独立并且能充分反映总体信息,以这些新指标为自变量进行多重回归就不会再出现共线性的困扰,便于进一步分析。
主成分回归是一种线性回归有偏估计,针对线性回归模型自变量间存在多重共线性时,替代最小二乘法,以获得回归系数的估计。
该算法的基本原理是先采用主成分分析将原变量转换成若干个主成分,各个主成份之间互相独立,它们将相关性较强的变量综合在同一个主成分中,这些主成分从不同侧面反映原变量的综合影响,原则是原变量的信息不致过多损失。接着以这些主成分为自变量进行多重回归,再根据主成分与因变量之间的对应关系,求得原回归模型的估计方程。
输出结果:
主成分个数选择信息表:给出用户选择的判别条件。
主轴(对应主成分)信息表:给出各个主成份对应的统计量和组成,各主成份所占的贡献率及累计贡献率;
自变量相关系数表:给出了各变量间相关系数表。
回归系数表:给出模型的回归系数列表;
模型分析表:给出了最终模型的检验,修正的R平方越接近1,模型估计效果越不错。
回归方程:给出了的算法得出的回归方程。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1590****658 | 2018-09-09 21:15:18 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:48:09 | 1年 | Windows | 单机版 |
| 1362****882 | 2018-01-27 11:49:16 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1528****175 | 2017-06-15 14:23:53 | 1年 | Windows | 单机版 |
| 1803****455 | 2017-05-19 03:28:32 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-07 00:10:41 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-06 22:57:30 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:36 | 1年 | Windows | 单机版 |