
以数据文件“马克威通用数据3.mkw”为例,演示岭回归算法的操作说明。该数据表示了某地抽样调查29例儿童的血红蛋白与4种微量元素的含量的结果,分析可否用4种微量元素(钙、镁、铁、铜)来预测血红蛋白的含量。
(1)首先,在工作区,打开建模分析工作流“高级统计”→“回归分析”→“岭回归”。
(2)接着选择数据源;
(3)然后设置算法的参数;
(4)具体操作及应用如下
(1)选择变量参数
选择“训练”功能;其中各参数变量的说明如下:
输入变量:输入自变量和因变量;
岭回归参数K的选取:选择岭回归参数K的方法;
岭迹分析图:输出岭迹分析图;
缺失值处理:包含两种处理方法,即添加列均值填充和删除缺失值所在行;
模型保存:选择模型保存的路径,用于预测。
设置好参数如下所示,因变量为“血红蛋白”,自变量为“钙”、“镁”、“铁”、“铜”,参数部分K=0.5:


(2)输出结果:
岭回归方程:

自变量相关系数:

模型分析表:

(3)结果说明:
岭回归方程给出了岭回归模型在岭迹k=0.5下的,可用来预测样本数据的方程表达式;同时自变量相关系数表给出自变量之间的相关性大小,可以看出例子中的变量之间的相关性都不是特别强,但也不能忽略相关性;模型分析表中给出的R平方和修正的R平方值显示该模型的准确度很好。
(1)选择“应用”选项,界面切换到预测设置,到“模型训练”时模型的保存路径下打开模型,其中各参数的说明如下:
模型来源:选择回归训练所建的模型。注:当且仅当训练时指定K值,模型才应用于预测;
变量设置:分为“选择变量”和“输入变量”;其中后者允许用户修改变量;
预测方法:当监理模型的方式为“输入变量”时,预测的方法包括静态和动态预测法。
参数设置如下所示:

(2)输出结果:
岭回归预测结果:

(3)结果说明:
岭回归预测结果可以得到对原始数据的拟合结果,可对比实际值,观测预测的数据是否准确。
输入变量类型:整型、浮点型
输入数据尺度:标量型
岭回归是专门用于共线性数据的有偏估计回归方法。其实质是改良的最小二乘法,以放弃最小二乘的无偏性,损失部分信息,放弃部分精确度为代价来寻求效果稍差,但更符合实际的回归方程。
可应用的情况包括:数据点少于变量个数、所有变量之间有较强的线性相关性、变量之间的数据变化比较小、部分变量之间有线性相关等。
岭回归为了避免最小二乘法中矩阵计算 的行列式接近于零,而使得计算误差太大,所以在矩阵的主对角元素都加上一个K值,降低矩阵计算奇异的风险。矩阵可以表示为:
的行列式接近于零,而使得计算误差太大,所以在矩阵的主对角元素都加上一个K值,降低矩阵计算奇异的风险。矩阵可以表示为:

B(K)为回归方程组 的最小平方解;它的值随着K的改变而改变,这个值就称为岭迹,我们可以根据岭迹图的平稳性确定K的取值。
的最小平方解;它的值随着K的改变而改变,这个值就称为岭迹,我们可以根据岭迹图的平稳性确定K的取值。
所以岭回归主要在于参数K的选取;用户可以自定义指定的K值大小,也可以系统自动选择,系统自选的方法有:
利用方法Hoerl和Kennard(1970):

利用方法Lawless和Wang(1975):

利用方法Hoerl和Baldwin(1975):

利用方法均方误差H(k)最小法:

K值选取的原则:尽可能小的k使得参数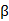 的估计值尽量稳定下来。
的估计值尽量稳定下来。
输出结果:
模型说明:给出数据源信息、训练的变量名和有效训练记录数;
岭回归方程:给出因变量与自变量的回归方程;
岭参数K的取值:给出模型的K值;
自变量相关系数表:给出自变量之间的相关系数,可由此观测到变量之间的相关程度大小;
回归系数表:给出自变量系数和常数项的标准误差等统计量;
方差分析表:给出回归、残差和总离差的平方和,自由度均方,F和P值等统计量;
模型分析:给出R平方和修正的R平方值;可由这两个值观察模型的准确度;
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1536****053 | 2023-10-24 16:09:05 | 1年 | Windows | 单机版 |
| 1591****808 | 2023-10-24 16:06:02 | 1年 | Windows | 单机版 |
| 1536****053 | 2023-10-24 16:01:26 | 1年 | Windows | 单机版 |
| 1530****827 | 2019-05-28 21:43:01 | 1年 | Windows | 单机版 |
| 1301****055 | 2018-11-24 19:29:50 | 1年 | Windows | 单机版 |
| 1884****551 | 2018-09-17 11:11:31 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:52:02 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1528****175 | 2017-06-15 14:23:53 | 1年 | Windows | 单机版 |