
以数据文件“马克威通用数据3.mkw”为例,演示二值逻辑回归算法的操作说明。该数据分析患者是否感染与失血等因素的关系,在工作区,打开建模分析工作流:“高级统计”→“回归分析”→“二值逻辑回归”。
(1)选择变量参数
选择“训练”功能;其中各参数变量的说明如下:
交互作用:用于选入自变量的交互作用;先选中需要交互的两个或多个变量,然后点击按钮即可;
分类变量:用于设置哑变量的取值方式,哑变量可分析多个不存在线性关系的多分类变量;
分类变量编码方法:设置编码方法,包括:Effect和Reference;
临界值:设置拟合临界值,用于评估模型;
模型保存:选择模型的保存路径,用于预测。
参数设置如下所示,因变量设置为“是否找到工作”,协变量设置为“是否独生子女”、“期望薪酬”、“花费时间”、“学校层次”、“家庭收入水平”:


(2)输出结果:
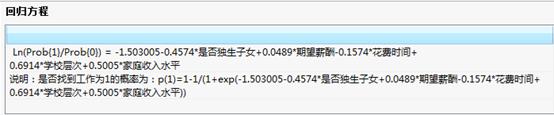
回归方程:
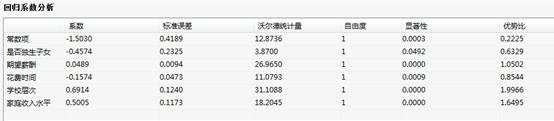
回归系数分析:
ROC曲线

Gain图
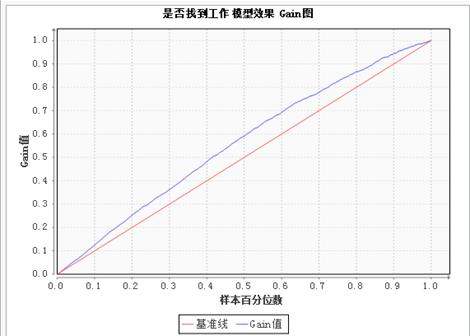
Lift曲线
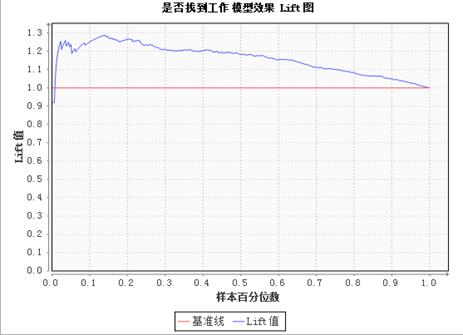
(3)结果说明:
输出结果有回归方程、回归系数分析、ROC曲线图、Gain曲线图、Lift曲线图等。
(4)选择“预测”选项,界面切换到预测设置,到“模型训练”时模型的保存路径下打开模型,其中各参数的说明如下:
模型来源:选择训练模型保存的路径;
变量设置:匹配变量,用户根据需要可以修改匹配项;
临界值:设置预测回判临界值,用于模型的评估。
设置好参数如下所示:

(5)输出结果:
二值逻辑回归预测:

(6)结果说明:
给出二值逻辑回归预测对于未知数据样本的回归预测,将这些数据根据已训练的模型分类;从表中是否感染回判值可以看出:当预测值大于设定的临界值,则返回1,否则返回结果0。
因变量必须是布尔型,自变量可以为除字符型、布尔型以外的任何类型。
二值逻辑回归用于研究某个二值随机事件发生的概率与某些因素之间的关系。其自变量可以是连续变量、二分类变量和多值分类变量;对于多于两个值的随机变量(包括连续型随机变量),需要设置哑变量进行分析,哑变量可以把多值分类自变量处理成类似二分类变量,也可以用二值逻辑回归来分析。
二值逻辑回归广泛应用于研究二分类(有序、无序)的因变量与自变量的关系。但逻辑回归与线性回归返回预测值不同,它主要是根据回归方程预测某个结果出现的概率。
对逻辑回归不能采用最小二乘法估计参数,而应使用极大似然估计或迭代加权的最小二乘法估计。因为极大似然估计正是应用于概率论上的参数估计,符合对因变量的概率预测。它的思想是:如果所选参数能使样本出现的概率最大,则可直接认为这个参数就是估计的真实值。下面给出回归的模型:
假设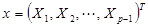 代表自变量,
代表自变量,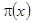 表示因变量取值为“真”的概率,对
表示因变量取值为“真”的概率,对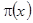 作如下变换:
作如下变换:
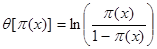
建立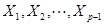 与
与 的线性函数,即
的线性函数,即
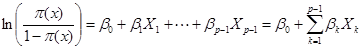
或
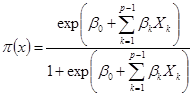
我们称后面两式为线性Logistic回归模型,或简称Logistic模型。
输出结果:
回归方程:给出自变量与因变量之间的概率数学表达式;
回归系数分析:分析常数项和自变量的估计系数的标准误差、自由度、置信区间等统计量;
回归模型评价:给出-2对数似然值、CSR平方和NKR平方值;
二值逻辑回归预测:给出实际数据的拟合值;
ROC曲线:给出ROC曲线;
分类表:给出预测值与实际值的分类结果,以及分类正确率。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1576****682 | 2023-03-09 08:04:26 | 1年 | Windows | 单机版 |
| 1881****083 | 2020-11-24 20:53:23 | 1年 | Windows | 单机版 |
| 1381****835 | 2018-11-25 03:38:20 | 1年 | Windows | 单机版 |
| 1884****551 | 2018-09-17 11:11:31 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:52:02 | 1年 | Windows | 单机版 |
| 1840****220 | 2018-06-01 09:31:08 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1590****190 | 2017-06-21 13:42:04 | 1年 | Windows | 单机版 |
| 1803****455 | 2017-05-26 01:24:10 | 1年 | Windows | 单机版 |