
以数据文件“马克威通用数据3.mkw”为例,演示概率单位回归算法的操作说明。该数据为研究某毒素的毒力,观察给药一小时,老鼠的死亡情况。
(1)首先,在工作区,打开建模分析工作流“高级统计”→“回归分析”→“概率单位回归”;
(2)接着选择数据源;
(3)然后设置算法的参数;
(4)其中各类参数的含义为:
反应频数变量:选入该栏的变量用来表示对实验刺激做出反应(如死亡例数)的观察对象的数目。
总观测数:用于选入接受实验刺激的总观察单位例数,取值不能小于反应频数变量的取值。
分层变量:选入分组变量。
协变量:选入一个用来表示不同试验刺激条件的变量(如用药的剂量)。
自然响应率:用于选择在模型中是否预先设置自然响应率。自然响应率表示没有刺激条件时(即不给药时)结局事件的自然发生概率。它包括以下三个选项:
无自然响应率:即不设置自然响应率。
从数据中计算:从现有的数据中计算自然响应率,即依据现有数据计算在没有刺激条件下的响应频率来估计自然响应比率。
指定为常数:如果从以前的研究中已知自然响应率的大小,则在此处将其键入,默认值为0.01。
最大迭代次数:系统默认值为50次,用于控制计算。当算法迭代到最大迭代次数时,如果此时算法未收敛,则跳出循环。
设置好参数如下所示:

(5)输出结果:
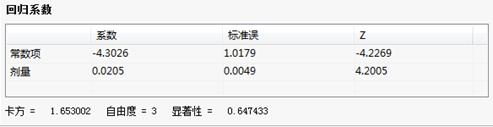
回归系数表:
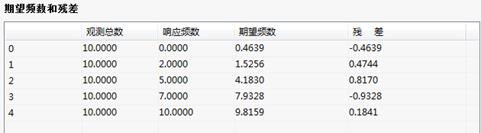
期望频数和残差:
(6)结果说明:
回归系数表给出了协变量的系数、系数的Z值、卡方值、以及显著性,期望频数和残差表列出的为各剂量组的观测值、期望值以及残差。表中第一栏列出的为试验剂量变量。
输入变量类型:整型、浮点型
(注:取值不能为负,反应数不大于总观测数)
输入数据尺度:标量型
概率单位回归主要用于分析实验的刺激强度和反应比例之间的关系。其目的是得到达到某一反应比例所需要的刺激强度。概率单位回归分析广泛应用于医学研究领域,尤其是毒理学研究中,常需要进行剂量-反应关系研究,从而求得半数有效量或半数致死量。
概率单位回归方程是将概率转换为与自变量所对应的标准正态离差,将因变量的响应率作逻辑转换,以便于求解。
概率单位回归模型主要是针对定性(两态或多态的)因变量而提出的回归分析法。模型响应概率为:

其中: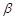 :为参数估计向量
:为参数估计向量
F:为累积分布函数(正态的、logistic等)
X:为自变量向量
p:响应概率
C:自然(阀值的)响应比率,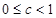 ;可以取固定值,也可以估计;c=0是常用的模型
;可以取固定值,也可以估计;c=0是常用的模型
对模型的响应概率方程参数的估计可以通过以下方法:对参数C的估计,可直接通过模型估计出来,这种方法为:计算模型对数似然函数的二阶导数矩阵,即求解黑塞矩阵。对参数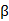 的极大似然估计,可由Nenwfon-Raphso迭代算法计算。
的极大似然估计,可由Nenwfon-Raphso迭代算法计算。
输出结果:
回归系数表:给出模型的概率单位回归方程,及其卡方、自由度、显著性,由此得出模型的拟合优度。
期望频数和残差表:列出的为各剂量组的观测值、期望值以及残差,表中第一栏列出的为试验剂量变量。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1811****398 | 2018-07-23 13:52:02 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1803****455 | 2017-05-26 01:24:41 | 1年 | Windows | 单机版 |
| 1803****455 | 2017-05-19 16:23:44 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-07 00:10:41 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-06 22:57:30 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:43 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:39 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:16 | 1年 | Windows | 单机版 |