
(1)以数据文件“马克威通用数据1.mkw”为例,选取前50条数据演示Q-Q图的操作。首先,在工作区内,打开建模分析工作流:“数据制图”→“Q-Q图”,接着选择数据源,然后设置算法参数,最后双击运行按钮;
其中各类参数的含义为:
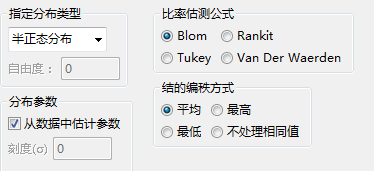
指定分布类型:用于指定待检验的分布,包括Beta分布、卡方分布、指数分布、Gamma分布、半正态分布、拉普拉斯分布、Logistic分布、对数正态分布、正态分布、Pareto分布、T分布、Weibull分布和均匀分布等。针对某些分布需要设置自由度等必要参数。
分布参数:如果选中“从数据中估测参数”,则自动从数据中估测参数,并且输出参数,不选择该项,则可自行选择参数。
比率估计公式:提供了四种计算比例的方法,每次只能选择其中一项,以下公式中n是观测量的数目,r是从1至n的秩次。
Bloom:公式为(r-/3/8)/(n+1/4)
Rankit:公式为(r-1/2)/n
Tukey:公式为(r-1/3)/(n+1/3)
VarDerWaerden:公式为r/(n+1)
结的编秩方式:指定如何对结编秩。“结”指是值相同观察数据。系统提供取平均、最高、最低和不处理相同值四种对结的编秩方法。
参数设置如下所示,变量选择“购买总额”:
(2)输出结果
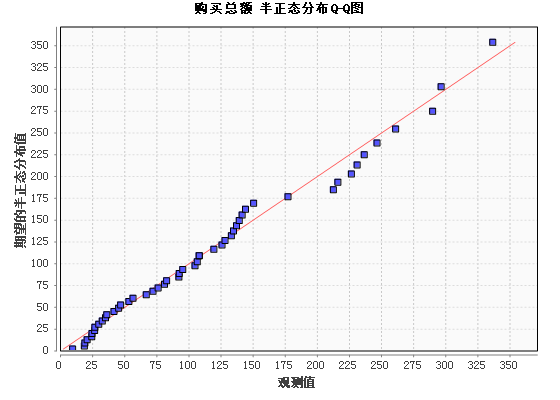
正态分布Q-Q图:
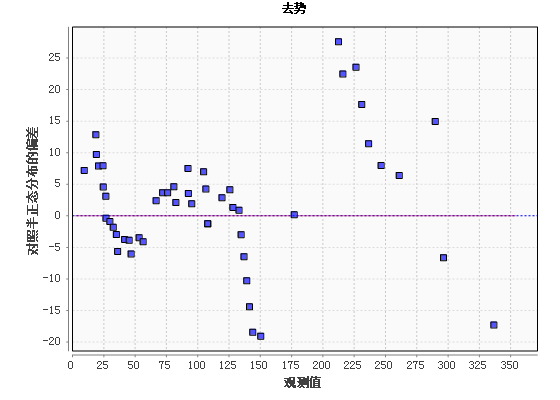
去势Q-Q图:
(3)结果说明
如果数据服从某种分布,则在Q-Q分布图中,数据点应基本在图中对角线上;同时Q-Q去势分布图中,数据点应在一个较小的区域中。如本例Q-Q去势分布图中,数据点都控制在一定的范围内,可以认为数据服从半正态分布。
输入变量类型:数值型,如整型、浮点型、布尔型
Q-Q图通过描述变量数据分布与指定分布的分位数之间差别的曲线,来反映所分析的数据是否符合指定分布。
Q-Q图在绘制为比较两个概率分布的散点图时;先选择一系列概率值,对每个概率值分别计算其在两个分布上的分位数作为画图点的坐标。
输出结果:
Q-Q图:给出Q-Q图,观察数据是否服从正态分布;
去势Q-Q图:观察数据的分布范围及其服从的分布。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1513****706 | 2021-07-05 19:04:26 | 1年 | Windows | 单机版 |
| 1786****007 | 2021-07-05 16:26:28 | 1年 | Windows | 单机版 |
| 1305****178 | 2019-12-27 19:47:09 | 1年 | Windows | 单机版 |
| 1589****975 | 2019-03-06 12:54:53 | 1年 | Windows | 单机版 |
| 1840****220 | 2018-06-01 09:31:08 | 1年 | Windows | 单机版 |
| 1801****513 | 2018-04-07 13:53:02 | 1年 | Windows | 单机版 |
| 1891****338 | 2018-01-26 20:54:33 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 12:17:53 | 1年 | Windows | 单机版 |
| 1881****602 | 2017-08-07 17:44:36 | 1年 | Windows | 单机版 |