
(1)以数据文件“马克威通用数据1.mkw”为例。首先,在工作区内,打开建模分析工作流:“数据制图”→“自相关图”,接着选择数据源,然后设置算法参数,最后双击运行按钮。
其中各类参数的含义为:
变量:将被描述的数值型变量选入本框中。如果选入多个变量,系统将分别对每个变量输出它们的自相关图和偏自相关图。
自相关:选定本选项时,系统将生成自相关系数的图形。
偏自相关:选定本选项时,系统将生成偏自相关系数图形。
差分阶数:指定序列差分阶数。
最大滞后数:指定需要计算自相关和偏自相关的最大的滞后数。
参数设置如下所示,选择变量为“sodium”:
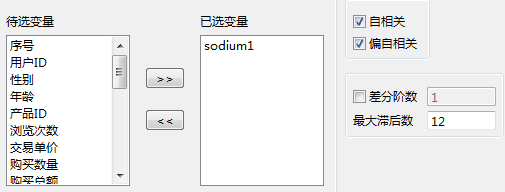
(2)输出结果
偏自相关图:
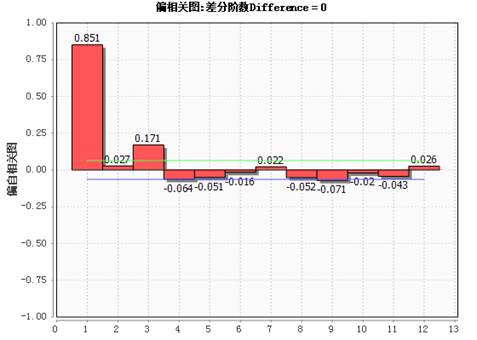
偏相关表:
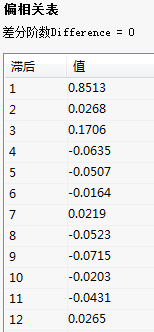
自相关图:
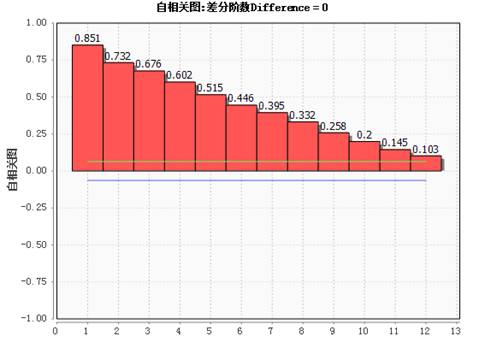
自相关表:
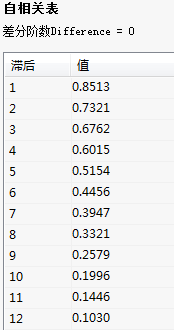
(3)结果说明
从结果中我们可以看到自相关图是拖尾的,偏自相关图是截尾的;那么可以粗略的判断这些数据应该是属于AR模型。从偏自相关图可以看出,在一阶之后的项都趋于0,所以AR模型的阶数可暂定为1,即用AR(1)来分析数据。
输入变量类型:数值型,如整型、浮点型、布尔型
自相关图是时间序列的一种图形观察工具,通过描绘序列和自身的提前或滞后序列间的相关系数、偏自相关系数来反映系统参数对系统影响以及系统的稳定性状况。
自相关图展现的结果包括ACF和PACF两种类型,它们都用于描述单个时间序列的情况。
ACF(自相关函数)
ACF可以作为判断时间序列平稳性的工具,如果ACF图中,随着滞后阶数的增大自相关系数不是迅速减小,则要考虑时间序列是否不平稳,是否需要继续差分的必要。同时,ACF是不能计算负值的,这需要用原序列经过数据处理再来做。
PACF(偏自相关函数)
PACF从高阶开始,逐个检验每阶的偏自相关系数是否有意义,直到第一个有意义的为止,这时的阶数就是模型中应该包含的最大阶数。
输出结果:
偏自相关图:给出测量值的偏自相关图,显示系统参数对系统稳定性的影响;
自相关图:给出测量值的自相关图,反映系统的稳定性状况。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1305****178 | 2019-12-27 19:47:09 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 12:17:53 | 1年 | Windows | 单机版 |
| 1307****061 | 2017-06-09 00:31:13 | 1年 | Windows | 单机版 |
| 1860****541 | 2017-05-07 18:28:13 | 1年 | Windows | 单机版 |
| 1376****104 | 2017-05-04 11:53:58 | 1年 | Windows | 单机版 |
| 1340****082 | 2017-04-07 09:51:47 | 1年 | Windows | 单机版 |
| 1340****082 | 2017-04-07 09:51:47 | 1年 | Windows | 单机版 |
| 1340****082 | 2017-04-07 09:30:05 | 1年 | Windows | 单机版 |
| 1340****082 | 2017-04-07 09:30:05 | 1年 | Windows | 单机版 |