
(1)以数据文件“马克威通用数据1.mkw”为例,演示两个相关样本检验算法的演示。
首先,在工作区内,打开建模分析工作流:“基础分析→非参数检验→两个相关样本检验”,接着选择数据源,然后设置算法的参数,最后点击运行按钮。其中各类参数的含义如下:
变量表:待检验的两个相关样本。在选项表中选择两个变量,添加到变量表。系统支持的数据类型有:浮点型、整型、布尔型。
检验类型:选择检验的方法。
对变量“sodium1、sodium2”进行两个相关样本检验。具体的参数设置如下所示:
 图 0-1 两个相关样本检验-属性设置
图 0-1 两个相关样本检验-属性设置
从选项列表同时选择变量“sodium1”和“sodium2”到测试配对变量列表,选中威尔科克森配对秩和检验复选框。
(2)输出结果
 图 0-2 两个相关样本检验-树形结果列表
图 0-2 两个相关样本检验-树形结果列表 图 0-3 两个相关样本检验-秩-威尔科克森配对秩和检验
图 0-3 两个相关样本检验-秩-威尔科克森配对秩和检验 图 0-4 两个相关样本检验-威尔科克森配对秩和检验
图 0-4 两个相关样本检验-威尔科克森配对秩和检验
(3)结果说明
从结果得出:两个相关样本Z统计量的值是-3.4156,检验的P值(0.0006)小于0.05,因此,拒绝零假设,认为两个变量有显著性的差异。
输入变量表数据类型:整型、浮点型、布尔型
输入数据尺度:标量型、名义型、有序型
两个相关样本的检验,是在对两个相关总体分布不甚了解的情况下,检验两个相关样本来自的两个总体分布是否存在显著性差异。
本系统提供了三种检验方法,原理如下:
符号检验
两个相关样本的符号检验利用正、负符号个数的多少进行检验。如果正负的个数大致相当,则两个相关样本数据分布差距较小;若正负的个数相差较多,则两个相关样本数据分布差距较大。因为在零假设前提下,两个相关样本中的S+和S- 的分布时概率值为0.5的二项分布。为精确计算,系统自动根据S+ 、S-和n计算实际的概率值,如果该概率值小于或等于给定的显著性水平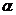 ,则不能拒绝H0,认为样本来自的两个配对总体的分布无显著差异。
,则不能拒绝H0,认为样本来自的两个配对总体的分布无显著差异。
威尔科克森配对秩和检验
Wilcoxon配对秩和检验按照符号检验的方法,分别将第二组的各个变量值减去第一组样本的各个变量值,如果差值为正则记为正号,差值为负记为负号,并同时保存绝对差值数据;然后,将绝对差值数据按升序排序,并求出相应的秩;最后,分别计算正号秩总和W+、负号秩总和W-以及正号平均秩和负号平均秩。可以直观地理解,如果正号平均秩和负号平均秩大致相当,则可以认为两配对样本数据的正负变化程度基本相当,两配对总体的分布无显著差异。
为作精确判断,系统根据正、负号平均秩计算出Z统计量并给出检验的P值。如果显著性小于或等于给定的显著性水平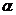 ,则拒绝H0,认为样本来自的两个配对总体的分布有显著差异。
,则拒绝H0,认为样本来自的两个配对总体的分布有显著差异。
麦克尼马尔检验
McNemar检验是一种变化显著性检验,它将研究对象自身作为对照者,采用二项分布检验,研究其“前后”的变化是否显著。如果检验的P值小于或等于给定的显著性水平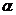 ,则拒绝H0,认为样本来自的两个配对样本总体的分布有显著性差异。
,则拒绝H0,认为样本来自的两个配对样本总体的分布有显著性差异。
需要注意的是,McNemar检验分析的变量是二值变量。因此,在实际应用中,如果变量不是二值的,应首先对数据进行二值化处理。
输出结果:
检验结果:列出不同类型的检验结果,依据P值判断相关样本的总体差异。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1886****092 | 2018-09-02 10:13:17 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:48:09 | 1年 | Windows | 单机版 |
| 1840****220 | 2018-06-01 09:31:08 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-07 00:10:41 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-06 22:57:30 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:20 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:17 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:13 | 1年 | Windows | 单机版 |