
(1)以数据文件“马克威通用数据1.mkw”为例,演示多个独立样本检验算法的操作。
首先,在工作区内,打开建模分析工作流:“基础分析→非参数检验→多个独立样本检验”,接着选择数据源,然后设置算法的参数,最后点击运行按钮。其中各类参数的含义如下:
变量表:系统支持的数据类型包括浮点型,整型,布尔型。
分组变量:用来把参与运算的样本进行分类的变量。通过指定分组变量的取值,来确定变量的分类。多个独立样本检验要求指定分组变量的两个取值(最小值、最大值)把参与运算的变量分为几类。当然分组变量本身取值可以有多个类别,只有属于指定的分组取值的样本才参与计算。
检验类型:选择检验的方法。
对变量“购买总额”进行多个独立样本检验,其分组变量为“用户喜好”。具体的参数设置如下所示:
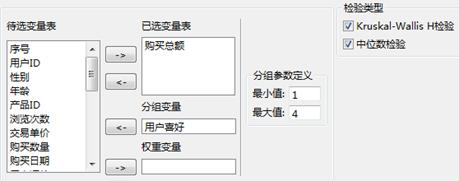 图 0-1 多个独立样本检验-属性设置
图 0-1 多个独立样本检验-属性设置
在检验类型中,本例将克拉夏尔-瓦里斯检验和中位数检验复选框全选中,以利于对照这两种方法。
(2)运行结果
 图 0-2 多个独立样本检验-树形结果列表
图 0-2 多个独立样本检验-树形结果列表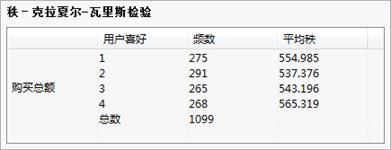 图 0-3 多个独立样本检验-秩-克拉夏尔-瓦里斯检验
图 0-3 多个独立样本检验-秩-克拉夏尔-瓦里斯检验 图 0-4 多个独立样本检验-秩-克拉夏尔-瓦里斯检验
图 0-4 多个独立样本检验-秩-克拉夏尔-瓦里斯检验 图 0-5 多个独立样本检验-中位数检验
图 0-5 多个独立样本检验-中位数检验
(3)结果说明
从表中可以看出克拉夏尔-瓦里斯检验所得出的P值(0.7353)和中位数检验所得出的P值(0.7623)均大于显著性水平0.05,因此应接受零假设,认为不同喜好的顾客购买总额不存在显著性差异。
输入变量表数据类型:整型、浮点型、布尔型
输入数据尺度:标量型、名义型、有序型
多个独立样本检验推断取得独立样本的多个总体的分布是否存在显著性差异,即通过对多个独立样本的均值、中位数等进行差异检验,来分析它们是否来自相同的分布。多个独立样本是指按独立抽样方式获得的多组样本。
系统提供了常用的克拉夏尔-瓦里斯检验法和中位数检验法两种方法。
克拉夏尔-瓦里斯检验法
即Kruskal-Wallis检验,其实质是两个独立样本的曼-惠特尼U检验在多个样本下的推广,用于检验多个总体的分布是否存在显著差异。首先,将各独立样本混合后按升序排序,求出各变量值的秩,然后考察各组秩的均值是否存在显著差异。系统通过K-W统计量来反映平均秩间的差异。根据给出的显著性水平,若检验的P值小于该显著性水平,则拒绝零假设,认为多个独立样本来自的多个总体分布存在显著性差异。
中位数检验法
中位数检验通过对多个独立样本的分析,检验他们来自的总体的中位数是否存在显著差异。如果样本来自的总体分布无显著差异,即多个总体有共同的中位数,那么这个共同的中位数应该处于每组样本数据的中间位置上,也就是说,每组样本中大于或小于该中位数的样本数应大致相同。通过分析样本间中位数位置的差异程度,可以判断它们是否来自相同的总体。系统用卡方统计量来度量这一差异程度。
输出结果:
秩-克拉夏尔-瓦里斯检验:列出多个独立样本描述统计量和检验结果。
中位数检验:列出中位数检验结果。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1590****469 | 2021-09-22 14:24:34 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:48:09 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-07 00:10:41 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-06 22:57:30 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:42 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:27 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:23 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:05 | 1年 | Windows | 单机版 |