
(1)以数据文件“马克威通用数据1.mkw”为例,演示配对双样本均值检验算法的操作。
首先,在工作区内,打开建模分析工作流:“基础分析→参数检验→配对双样本均值检验”,接着选择数据源,然后设置算法的参数,最后点击运行按钮。
其中各类参数的含义如下:
变量表:需要同时选中两个变量方能添加至“已选变量表”。
置信度:设置置信度的值,要求为区间(0,1]之间任意值,系统默认为95%。
原假设:两总体均值差等于零,一般用H0表示。
备择假设:分为单侧检验和双侧检验。单侧检验分别为两总体均值差大于0或小于0;而双侧检验则是两总体均值差不等于0。
样本正态检验:检验样本是否服从正态分布,通常利用直方图和正态概率图两种图形来反映,这两种方法都是从主观上判断是否服从正态分布。在直方图中,利用直方图的分布与正态分布的密度函数曲线相比较,可以主观判断样本是否服从正态分布;在正态概率图中,正态概率线是一条Y=X的直线,根据散点在正态概率线周围分布情况来判断,当散点越集中在正态概率线的周围时,说明样本越接近正态分布。
对变量“浏览次数、购买数量”进行配对双样本检验。具体的参数设置如下所示:
 图 0-1 配对双样本均值检验-属性设置
图 0-1 配对双样本均值检验-属性设置
从左边的选项列表中,选择变量“浏览次数”和“购买数量”进入测试变量列表,设置备择假设以及置信度水平,双击“运行”节点,进入分析过程。
(2)输出结果
 图 0-2 配对双样本均值检验-树形结果列表
图 0-2 配对双样本均值检验-树形结果列表 图 0-3 配对双样本均值检验-统计
图 0-3 配对双样本均值检验-统计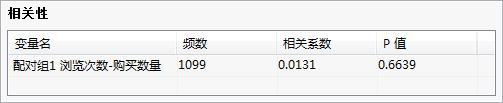 图 0-4 配对双样本均值检验-相关性
图 0-4 配对双样本均值检验-相关性 图 0-5 配对双样本均值检验-检验结果
图 0-5 配对双样本均值检验-检验结果
(3)结果说明
由统计表可见,总的记录数为1099人,以及他们的浏览次数和购买数量的均值、频数、标准差和均值标准误。
由相关性表可见,相关系数为0.6639,显著性为0.0131小于0.05,所以两组变量之间有相关关系。
由检验结果表可见,因为显著性为0.0000远小于0.05,因此认为两组变量有显著的不同。
输入变量表数据类型:整型、浮点型、布尔型
输入数据尺度:标量型、名义型、有序型
配对双样本均值检验用于检验两个相关的样本是否来自具有相同均值的总体。进行配对双样本均值检验要求被比较的两个样本具有配对关系,而且均值是对于检验有意义的描述统计量。
配对双样本均值检验,即用于进行配对的差值平均数与总体平均数比较的T检验。要求配对的样本满足:被比较的样本之间存在配对关系;两组样本均来自正态分布总体;均值是对于检验是有意义的统计量。
输出结果:
统计:列出样本的统计信息。
相关性:得到配对检验样本的相关系数,相关系数越大,相关性越高。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1811****398 | 2018-07-23 13:48:09 | 1年 | Windows | 单机版 |
| 1840****220 | 2018-06-01 09:31:08 | 1年 | Windows | 单机版 |
| 1398****741 | 2017-12-29 09:10:30 | 1年 | Windows | 单机版 |
| 1556****001 | 2017-08-10 23:45:25 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-07 00:10:41 | 1年 | Windows | 单机版 |
| 1381****657 | 2017-04-06 22:57:30 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:42 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:37 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:33 | 1年 | Windows | 单机版 |
| 1397****925 | 2017-03-29 10:56:30 | 1年 | Windows | 单机版 |