
以数据文件“马克威通用数据1.mkw”为例,演示模糊聚类算法的操作。因为考虑到计算时间问题,可以取数据的前50条进行分析。
首先,在工作区内,打开建模分析工作流:“机器学习”→“模糊聚类”,接着选择数据源,然后设置算法参数,最后双击运行按钮。
设置好参数如下,变量选择字段为“年龄”、“浏览次数”、“交易单价”、“用户喜好”、“到达天数”,等级数设置方式为“变量最大值”,置信水平设置为90%,同时输出冰柱图和谱系图:
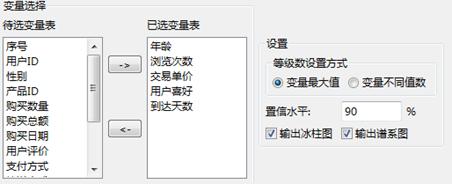 模糊聚类-属性设置
模糊聚类-属性设置
选项说明
输入变量:选择作为分类指标的变量,入选变量的数据类型要求为整形。
等级数设置方式:等级数设置方式有两个选项:变量最大值和变量不同数值。根据各变量的等级数对记录进行二值变量编码,当等级数设置方式为变量最大值时,各变量的等级数分别为各变量的最大值;当等级数设置方式为变量的不同数值时,各变量的等级数分别为各变量的不同取值数,当变量的最大值比较大时,如大于100,等级数设置方式应选择此项。
置信水平:设置置信水平,用于控制分类。系统默认值为0.8。
输出冰柱图和输出谱系图:指定输出的结果。
双击“运行”节点,系统进入分析过程,并在结果窗口输出如下:
 模糊聚类-树形结果列表
模糊聚类-树形结果列表 模糊聚类-聚类结果表
模糊聚类-聚类结果表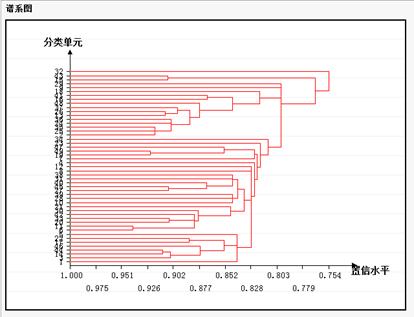 模糊聚类-谱系图
模糊聚类-谱系图
结果说明
分类表:给出了最终的分类结果。从表中知,从表中知,在置信度为0.9的水平,将所有的顾客信息聚成多类。
冰状图:当全体在置信水平小于0.754时,整个聚类过程的个数为1;当置信水平等于0.779时,整个聚类过程的聚类个数为2;当置信水平大于0.779且小于0.803时,整个聚类过程的聚类个数为3,依次类推,可以得到其他的聚类过程。
谱系图:可以用聚类谱系图展示置信度从1到0的动态聚类过程,样本各自为类,然后逐渐聚类以谱系连线表示聚在一起。
输入变量类型:数值型。
模糊聚类分析是将模糊集概念用到聚类分析中产生的,用来处理分类问题,它对各个领域中具有模糊特征的两态数据或多态数据具有明显的分类效果。该算法用在生物学、商业、经济、工程、信息科学、农业、医药学等许多领域,如区分气象灾害严重程度、地区气候湿润程度等问题。
模糊聚类算法根据研究对象本身的属性来构造模糊矩阵,在此基础上根据一定的隶属度来确定其分类系。系统的模糊聚类分析功能根据专家对研究对象的各指标进行打分得出原始数据。通过对原始数据进行变换、计算模糊相似矩阵、利用传递闭包法建立模糊等价矩阵,并根据给定不同的置信水平,求截阵等一系列过程对研究对象进行聚类得出模糊相似阵、分类关系阵和分类关系表。模糊聚类的具体算法过程如下:
1、对原始数据进行变换。变换方法通常有标准化变换、极差变换、对数变换。
2、计算模糊相似矩阵。选取在[-1,1]区间中的普通相似系数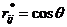 构成相似系数矩阵,
构成相似系数矩阵,
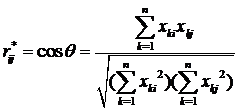
在此基础上做如下变换:
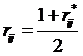
使得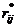 被压缩到[0,1]区间内,
被压缩到[0,1]区间内,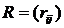 构成了一个模糊矩阵。
构成了一个模糊矩阵。
3、建立模糊等价矩阵。对模糊矩阵进行褶积计算: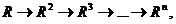 经过有限次褶积后使得
经过有限次褶积后使得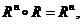 由此得到模糊分类关系
由此得到模糊分类关系 。模糊褶积的运算法则:设
。模糊褶积的运算法则:设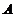 和
和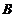 是
是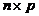 和
和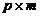 的模糊矩阵,则乘积
的模糊矩阵,则乘积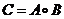 为
为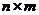 阵,其元素为:
阵,其元素为:
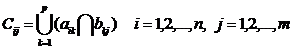
符号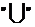 和
和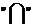 的含义是:
的含义是:
 ,
, 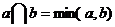
4、进行聚类。给定不同的置信水平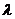 ,求
,求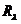 截阵,得到普通的分类关系
截阵,得到普通的分类关系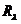 。当
。当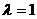 时,每个样品自成一类,随
时,每个样品自成一类,随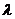 值的降低,由细到粗逐渐并类。
值的降低,由细到粗逐渐并类。
输出结果:
聚类结果表:列出对应于特定置信水平的分类结果。
冰柱分类图:显示样本集合依次在不同置信水平时的分类归属情况,左边对应为当前聚类的类别数,叉号则代表了哪几个样本可以聚在一类,样本间无叉号则表明在此处分类。
谱系图:显示样本集合置信水平从1到0时的动态聚类过程,横坐标是置信水平,起始点是1,终点是0;纵坐标是样本标号(注意仅仅指明标号,并不按某种顺序排序);红线指明样本间的聚类过程。
| 订购用户 | 订购时间 | 年限 | 运行环境 | 版本 |
| 1786****815 | 2023-03-10 14:12:48 | 1年 | Windows | 单机版 |
| 1833****189 | 2020-04-21 13:10:46 | 1年 | Windows | 单机版 |
| 1305****178 | 2019-12-27 19:47:09 | 1年 | Windows | 单机版 |
| 1335****121 | 2019-04-29 16:59:27 | 1年 | Windows | 单机版 |
| 1361****169 | 2019-04-01 17:30:32 | 1年 | Windows | 单机版 |
| 1801****427 | 2019-02-18 19:07:33 | 1年 | Windows | 单机版 |
| 1811****398 | 2018-07-23 13:13:07 | 1年 | Windows | 单机版 |
| 1580****630 | 2018-07-17 10:05:56 | 1年 | Windows | 单机版 |
| 1393****745 | 2018-02-25 10:39:20 | 1年 | Windows | 单机版 |
| 1885****897 | 2018-02-19 15:25:57 | 1年 | Windows | 单机版 |