
统计,顾名思义即将信息统括起来进行计算的意思,它是对数据进行定量处理的理论与技术。统计分析,常指对收集到的有关数据资料进行整理归类并进行解释的过程。在整个统计分析的过程中,分析是最重要的一个环节,如果缺少这一步,会降低统计工作的作用;准确的说,没有统计分析,统计的工作就没有活力、没有发展,也就没有统计工作的意义。
采用统计分析方法进行研究,必须遵循以下几个统计学基本特征:(1)科学性;(2)直观性;(3)可重复性
统计分析除了基础的统计分析外,还包含了高级统计的知识。高级统计一般包括:回归分析、聚类分析、时间序列、生存分析、判别分析、主成分分析、因子分析、协整分析、联立方程、面板数据模型等统计分析方法。这些高级统计分析不仅包含基础的变量统计信息,还能用于对数据的分类、聚类、回归及预测。可以说高级统计分析部分应用的范围更广、使用频率更高、实际解决问题的能力更强。
统计分析方法很多,但基本方法是定量分析。然而仅仅定量分析还是不足以解决问题,所以应遵循一定的分析技巧,统计分析技巧可以按照“定性—定量—定性”的顺序,巧妙的将定量分析和定性分析结合。
1.1.算法摘要
因子分析法是指从研究指标相关矩阵内部的依赖关系出发,把一些信息重叠、具有错综复杂关系的变量归结为少数几个不相关的综合因子的一种多元统计分析方法。因子分析是主成分分析的推广,但因子分析注重的是如何解释变量之间的共同变异问题,找出反应变量的共同因子和特定因子变量的线性函数,即用潜在的假想变量和随机影响变量的线性组合表示原变量,因子分析需要构造因子的模型。
基本思想是:根据相关性大小把变量分组,使得同组内的变量之间相关性较高,但不同组的变量不相关或相关性较低,每组变量代表一个基本结构即公共因子。
1.2.算法原理
应用因子分析法的主要步骤:1)对数据进行标准化处理;2)计算样本的相关矩阵R;3)求相关矩阵R的特征根和特征向量;4)根据系统要求的累积贡献率确定主因子的个数;5)计算因子载荷矩阵A;6)确定因子模型;7)根据上述计算结果,对系统进行分析。
因子分析算法中的各因子和原始变量之间的关系可以表示成矩阵的形式
X=AF+E,其中A为因子负荷矩阵,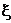 为残差向量。因子f1, f2, ..., fn之间互不相关即正交,因子分析就是要求出因子负荷系数矩阵A,并挑出负荷较大的前几个因子作为综合指标,然后根据这几个综合指标对个体进行打分评价。一般的可以通过EM算法估计求解残差向量和因子负荷系数矩阵;需要注意的是因子负荷系数矩阵A并不唯一,通过正交变换(或斜交变换)可以使综合指标变得容易解释。
为残差向量。因子f1, f2, ..., fn之间互不相关即正交,因子分析就是要求出因子负荷系数矩阵A,并挑出负荷较大的前几个因子作为综合指标,然后根据这几个综合指标对个体进行打分评价。一般的可以通过EM算法估计求解残差向量和因子负荷系数矩阵;需要注意的是因子负荷系数矩阵A并不唯一,通过正交变换(或斜交变换)可以使综合指标变得容易解释。
因子分析是研究从变量中提取共性因子的统计技术,最早由英国心里学家C.斯皮尔曼和K.皮尔逊提出,目的是定义和测定智力。他发现学生的各科成绩存在相关性,某一科成绩好的学生,往往其他科也比较好,从而推想是否存在某些潜在的共性因子,或某些一般智力条件影响学生的学习成绩。
三相关应用在商业(如市场细分)、医学药理分析、心理学、经济学、生物学(如农作物生长的影响因素分析)、社会学、地质分析等科学领域以及社会生产中,因子分析都得到了广泛应用。
四参考资料1.维基百科;
2.百度;
3.MBA智库百科(http://wiki.mbalib.com/)
4.马克威分析系统使用教程,www.tenly.com。
5.应用多元分析(第三版),王学民编著,上海财经大学出版社。
五实例假设某一社会经济系统问题,其主要特征可用4个指标表示,他们分别是生产、技术、交通和环境。其相关矩阵为:

相应的特征值、占总体百分比和累计百分比如下表:
| 编号 | 特征值 | 占总体百分比 | 累计百分比 |
| 1 | 2.49 | 62.25% | 62.25% |
| 2 | 1.13 | 28.25% | 90.50% |
| 3 | 0.35 | 8.74% | 99.24% |
| 4 | 0.031 | 0.76% | 100% |
对应特征值的特征向量为:

如果要求所取特征值反映的信息量占总体信息量的90%以上,则从累计特征值所占百分比看,只需取前两项即可。也就是说,只要两个主要因子。同时对应前两个特征值的特征向量,可求得其因子载荷矩阵A为:

于是,该问题的因子模型为:
X1=0.6f1+0.71f2;X2=0.85f1+0.38f2;X3=0.93f1-0.32f2;X4=0.74f1-0.40f2
由以上可以看出,两个因子中,f1是全面反映生产、技术、交通和环境的因子,而f2只反映了对生产和技术亮相增长有利,而对交通和环境增长却是不利的。也就是说,从相关矩阵分析的结果得到的是如果生产和技术都随着f2增长了,将来可能出现交通紧张和环境恶化的问题,f2反映了这两方面的相互制约状况。
六输入输出输入变量类型:要求数值型变量;如整型、浮点型(注:参与主成分分析的变量要求至少2个;数据要求没有缺损。)
输出结果:得到影响结果的互不相关的变量、特征根和累计贡献率等。
七相关条目主成分分析、因子旋转、因子载荷
八优缺点8.1.优点
1. 通过因子分析可以使用少数几个综合变量来代替原始多个变量,这些综合变量包含原始变量大部分信息,从而达到降维的效果;
2. 通过计算因子得分,能够对各个指标进行科学评价;
3. 因子分析在应用上侧重于信息贡献影响力综合评价;
4. 通过因子旋转使得因子变量更具有可解释性,命名清晰度高。
8.2.缺点
1. 计算因子得分时采用的是最小二乘法,此方法可能会失效。