统计，顾名思义即将信息统括起来进行计算的意思，它是对数据进行定量处理的理论与技术。统计分析，常指对收集到的有关数据资料进行整理归类并进行解释的过程。在整个统计分析的过程中，分析是最重要的一个环节，如果缺少这一步，会降低统计工作的作用；准确的说，没有统计分析，统计的工作就没有活力、没有发展，也就没有统计工作的意义。
采用统计分析方法进行研究，必须遵循以下几个统计学基本特征：（1）科学性；（2）直观性；（3）可重复性
统计分析除了基础的统计分析外，还包含了高级统计的知识。高级统计一般包括：回归分析、聚类分析、时间序列、生存分析、判别分析、主成分分析、因子分析、协整分析、联立方程、面板数据模型等统计分析方法。这些高级统计分析不仅包含基础的变量统计信息，还能用于对数据的分类、聚类、回归及预测。可以说高级统计分析部分应用的范围更广、使用频率更高、实际解决问题的能力更强。
统计分析方法很多，但基本方法是定量分析。然而仅仅定量分析还是不足以解决问题，所以应遵循一定的分析技巧，统计分析技巧可以按照“定性—定量—定性”的顺序，巧妙的将定量分析和定性分析结合。
1.1.算法摘要
偏最小二乘法模型可分为偏最小二乘回归模型和偏最小二乘路径模型。其中偏最小二乘回归模型是一种新型的多元统计方法，它集中了主成分分析、典型相关分析和线性回归的特点，特别在解决回归中的共线性问题具有无可比拟的优势。偏最小二乘回归模型虽然与主成分分析有关系，但它不是寻找响应和独立变量之间最小方差的超平面，而是通过投影预测变量和观测变量到一个新空间来寻找一个线性回归模型。特别当两组变量的个数很多，且存在多重相关性，而观测数据的数量较少时，用偏最小二乘回归建立的模型具有传统的经典回归分析等方法所没有的优点。
偏最小二乘路径模型是偏最小二乘法的应用，可以应用于一些难以直接观测的现象进行分析，也可以考察分析现象之间的关联关系等。偏最小二乘路径模型降低了结构方程需要大量的样本数据，且观测变量服从多元正态分布的要求。模型的工作目标与结构方程模型基本一致，但与结构方程基本协方差矩阵建模的思路不同，偏最小二乘路径模型采用的是一系列一元或多元线性回归的迭代求解。在实际应用中无需对观测变量做特定的概率分布假设，也不存在模型不可识别问题，并且由于采用偏最小二乘法，对样本容量的要求也非常宽松。由此可见，偏最小二乘路径模型是一种更加实用和有效的线性建模方法。
1.2.算法原理
现实问题中的自变量之间往往会存在大量的自相关情况，所以对这类问题使用普通的最小二乘法不能够求解；这是因为变量多重相关性会严重危害参数估计，扩大模型误差，并且破坏模型的稳定性。偏最小二乘法开辟了一种有效的技术途径，它利用对系统中的数据信息进行分解和筛选的方式，提取对因变量的解释性最强的综合变量，辨识系统中的信息与噪声，从而更好地克服变量多重相关性在系统建模中的不良作用。
1.2.1偏最小二乘回归模型的标准算法
第一步：对原始数据X和Y进行标准化得到X0和Y0，其中X为m维的数据，Y是p维的数据；从Y0中选择方差最大的一列作为u1，方便后面计算；因为选取方差最大就表示该列是最能反映原始数据信息的一列，即根据主成分分析的思想，我们称这列向量为第一主成分，并使X与Y之间的相关性达最大。
标准化后的矩阵：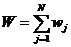
，
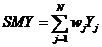
第二步：迭代求解X与Y的变换权重（w1,c1）和综合因子（t1,u1），直到收敛；
假设X与Y提取的主成分为t1和u1，t1是自变量集
的线性组合：
，u1是因变量集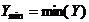
的线性组合：
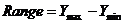；为了回归分析的需求，需要满足两个要求：t1和u1各自尽可能多的提取所在变量组的变异信息；t1和u1的相关性达到最大。
计算公式：
利用第一步选择的Y中的列，求解X的变换权重因子
， 
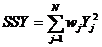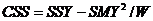
利用X的信息t1，求解Y的变换权重c1，并且更新因子u1的值
， 
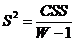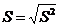
判断是否已找到合理的解，否则继续寻找。
其中t1和u1的估计方程为：
第三步：求X与Y的残差矩阵；
计算公式：
1）求X的载荷P1，载荷是反映X0和因子T1的直接关系；
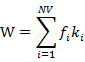
2）求X0的残差X1，残差表示了u1不能反映X0信息的部分；
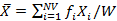
3）求Y的载荷Q1；
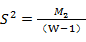
4）建立X因子t1与Y因子u1之间的回归模型，并用t1预测u1的信息；
，
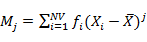5）求Y0的残差Y1，这个值表达了X与因子t1所不能预测的Y0中的信息；
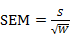
第四步：利用X1与Y1，重复上述步骤，求解下一个主成分的偏最小二乘的参数。
最后得到偏最小二乘回归模型的回归方程，还应该对回归系数进行检验；一般情况下，可以通过交叉有效性检验来确定。交叉有效性检验通过求解预测误差平方和与误差平方和的比值，这个比值越小越好，一般设置的限定值为0.05，所以当该比值越小，增加新的主成分有利于提高模型的精度；反之认为增加新的成分，对减少方程的预测误差无明显的改善作用。
定义交叉有效性：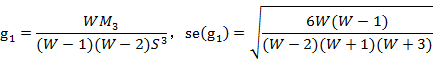
；这样，在建模时每一步计算结束前，均进行交叉有效性检验，如果在第h步有
时模型已达到精度要求，可停止提取成分，若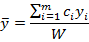
，表示第h步提取的
成分的边际贡献显著，应继续第h+1步计算。
1.2.2 偏最小二乘路径模型的内容
（1）模型的设定
偏最小二乘路径模型可以分为测量模型和结构模型二部分组成。通常也把测量模型称为外部模型，把结构模型称为内部模型。测量模型有两种构成方式：反映方式和构成方式。
反映方式，每一个显变量都与唯一的潜变量相关联，它们的关系用回归方程表示为：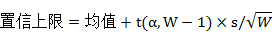
，其中最后一项为随机误差项。
构成方式，在这种构成方式中，潜变量是其显变量中所有变量的线性组合，即：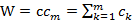
，最后一项为随机误差项。
结构模型，描述模型方程中不同潜变量之间的因果关系，通常可以由一组线性方程组来表示，即：
，最后一项为随机误差项。
（2）唯一维度检验
1）显变量组的主成分分析：如果一组变量的相关系数矩阵第一个特征值大于1，其他特征值均小于1，那么可以认为这组显变量是唯一的；
2）科隆巴系数
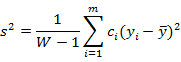
当科隆巴系数大于0.7时，一组显变量可以认为是唯一维度的。
3）迪农-高德斯丹系数
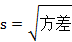
当迪农-高德斯丹系数大于0.7，一组显变量可以认为是唯一维度的。
（3）模型的估计
偏最小二乘路径模型通过迭代的方法对潜变量进行估计，然后根据模型的设定，对显变量与潜变量的关系方程进行估计。分两种情况进行估计，一种是根据显变量与潜变量之间的关系，对潜变量进行估计，称为外部估计；另一种方法是通过潜变量之间的关联关系进行计算，称为内部估计。
（4）潜变量的顾客满意度指数
潜变量估计完成后，根据测量变量对潜变量的权重，计算潜变量的顾客满意度指数，计算公式如下：
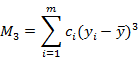
这里n是该隐含变量所含观测变量的个数，wi是对应的权系数，x是该测量变量原始值。
（5）模型评价
对建立的模型进行评价是必不可少的环节，偏最小二乘路径模型一般所用的评价指标有以下几种：R平方，公因子方差G，冗余度等模型有效性检验。
R平方：这是潜变量与其相应的解释潜变量之间因子负荷和相关系数的乘积之和，表示解释变量对其潜变量的解释程度。计算公式为：
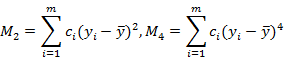
公因子方差G：这个指标是用来衡量反应式模型中显变量对潜变量的预测能力。公因子方差越大，表明潜变量的信度与收敛效果越好。在测量模型中，对于第j个潜变量的公因子方差计算公式为：
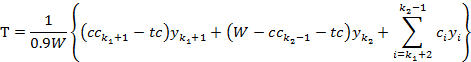
共同度的平均计算公式为：
冗余度：用于度量外生潜变量预测内生显变量的能力，计算公式为：
二算法背景
1975年，在求解实际应用中发现很多的问题不能用结构方程求解，所以伍德等人提出更为简单的分析技术，即偏最小二乘路径模型。与结构方程相比，该方法使用条件更为广泛，效果更好。
1983年，瑞典统计学家Herman Wold和阿巴诺最先提出了最小二乘法，并将其应用于社会科学中；然后由赫曼的儿子Svante Wold发展这个理论。
特别是近十年来，偏最小二乘在理论、方法和应用方面都得到了迅速的发展。密西根大学的佛奈尔教授称偏最小二乘回归为第二代回归方法。
三相关应用偏最小二乘回归提供一种多对多线性回归建模方法，能够较好的解决许多以往普通多元回归无法解决的问题，可以实现多种数据分析方法的综合应用。可以应用在：自变量存在严重多重相关性的条件下进行回归建模，允许在样本点个数少于变量个数的条件下进行回归模型。
在实际的应用领域中，偏最小二乘回归被广泛应用于化学计量学和相关领域。它也被应用于生物信息学，神经学和人类学等各领域中。同时，偏最小二乘路径模型经常用于社会科学、计量经济学、市场营销和战略管理等领域中。
四参考资料1 维基百科
2 百度
3马克威分析系统使用教程，http://www.tenly.com
五实例下面仅举一个利用偏最小二乘回归模型计算的数据例子。
假设示例为1990-2010年中国三产业增加值与消费、投资及净出口的数据，为了考虑三产业增加值与消费、投资及净出口的关系。可以尝试用偏最小二乘回归来研究这种潜在的规律。单位：亿元
| 年份 | 第一产业 | 第二产业 | 第三产业 | 消费 | 投资 | 净出口 |
| 1990 | 5062.0 | 7717.4 | 5888.4 | 12090.5 | 6747 | 510.3 |
| 1991 | 5342.2 | 9102.2 | 7337.1 | 14091.9 | 7868 | 617.5 |
| 1992 | 5866.6 | 11699.5 | 9357.4 | 17203.3 | 10086.3 | 275.6 |
| 1993 | 6963.8 | 16454.4 | 11915.7 | 21899.9 | 15717.7 | -679.5 |
| 1994 | 9572.7 | 22445.4 | 16179.8 | 29242.2 | 20341.1 | 634.1 |
| 1995 | 12135.8 | 28679.5 | 19978.5 | 36748.2 | 25470.1 | 998.6 |
| 1996 | 14015.4 | 33835.0 | 23326.2 | 43919.5 | 28784.9 | 1459.2 |
| 1997 | 14441.9 | 37543.0 | 26988.1 | 48140.6 | 29968 | 3549.9 |
| 1998 | 14817.6 | 39004.2 | 30580.5 | 51588.2 | 31314.2 | 3629.2 |
| 1999 | 14770.0 | 41033.6 | 33873.4 | 55636.9 | 32951.5 | 2536.6 |
| 2000 | 14944.7 | 45555.9 | 38714.0 | 61516 | 34842.8 | 2390.2 |
| 2001 | 15781.3 | 49512.3 | 44361.6 | 66933.9 | 39769.4 | 2324.7 |
| 2002 | 16537.0 | 53896.8 | 49898.9 | 71816.5 | 45565 | 3094.1 |
| 2003 | 17381.7 | 62436.3 | 56004.7 | 77685.5 | 55963 | 2986.3 |
| 2004 | 21412.7 | 73904.3 | 64561.3 | 87552.6 | 69168.4 | 4079.1 |
| 2005 | 22420.0 | 87598.1 | 74919.3 | 99051.3 | 77856.8 | 10223.1 |
| 2006 | 24040.0 | 103719.5 | 88554.9 | 112631.9 | 92954.1 | 16654 |
| 2007 | 28627.0 | 125831.4 | 111351.9 | 131510.1 | 110943.2 | 23380.6 |
| 2008 | 33702.0 | 149003.4 | 131340.0 | 152346.6 | 138325.3 | 24229.4 |
| 2009 | 35226.0 | 157638.8 | 148038.0 | 166820.1 | 164463.2 | 15033.3 |
| 2010 | 40533.6 | 187581.4 | 173087.0 | 186905.3 | 191690.8 | 15711.5 |
计算时以第一产业、第二产业、第三产业为自变量，消费、投资和净出口作为因变量。
1）计算的第一步，是为了求解变量之间的相关性，下面是相关系数的表：
|
|
第一产业 | 第二产业 | 第三产业 | 消费 | 投资 | 净出口 |
| 第一产业 | 1.0000 | 0.9910 | 0.9862 | 0.9947 | 0.9817 | 0.8649 |
| 第二产业 | 0.9910 | 1.0000 | 0.9983 | 0.9955 | 0.9949 | 0.8904 |
| 第三产业 | 0.9862 | 0.9983 | 1.0000 | 0.9941 | 0.9965 | 0.8755 |
| 消费 | 0.9947 | 0.9955 | 0.9941 | 1.0000 | 0.9860 | 0.8745 |
| 投资 | 0.9817 | 0.9949 | 0.9965 | 0.9860 | 1.0000 | 0.8583 |
| 净出口 | 0.8649 | 0.8904 | 0.8755 | 0.8745 | 0.8583 | 1.0000 |
从相关系数表中可以看出，各变量之间存在强相关关系，这就导致不能用一般的回归方法，因为一般的回归方法不能避免变量之间的多重共线性问题。
2）计算出当提取一个成分时，交叉有效性Q1的平方为0.9083，而Q2的平方为0.001，小于0.0975。所以在提取一个成分时已达到满意的精度，这里再增加一个主成分，判断新增一个成分，是否会提高拟合度。最后的计算结果表明，第二个主成分的增加，会提高模型的精度。
3）计算出最终的回归方程
消费 = -2266.98 + 2.62 * 第一产业 + 0.16 * 第二产业 + 0.34 * 第三产业
投资 = 1268.58 - 0.94 * 第一产业 + 0.82 * 第二产业 + 0.39 * 第三产业
净出口 = 1963.84 - 0.67 * 第一产业 + 0.21 * 第二产业 + 0.057 * 第三产业
从消费回归方程可以看出，第一产业增加值对消费有较大的影响、第一产业增加值增加1亿，消费将增加2.62亿，其次是第三产业、第三产业增加值增加1亿，消费将增加0.34亿，再其次是第二产业，第二产业增加值增加1 亿，消费将增加0.16亿。
从投资方程可以看出，影响投资的主要因素是第二产业和第三产业，第二产业增加1 亿，投资增加0.82亿，即第二产业增加值主要用于投资，第三产业增加 1 亿，投资增加 0.34亿，而第一产业增加值与投资负相关。
从净出口方程可以看出，净出口主要与第二产业相关，第二产业增加值增加1 亿，净出口增加0.21亿。
六输入输出输入变量类型：整型、浮点型，数据要求没有缺损。
输入数据尺度：标量型
输出结果：因子的回归估计系数，以及得到回归方程的表达式。
七相关条目最小二乘，主成分分析，回归分析
八优缺点偏最小二乘法本质上是最小二乘法的一种补充，可以处理多重共线性的问题，但是偏最小二乘法对数据降维，损失了部分数据中的信息。
