
统计,顾名思义即将信息统括起来进行计算的意思,它是对数据进行定量处理的理论与技术。统计分析,常指对收集到的有关数据资料进行整理归类并进行解释的过程。在整个统计分析的过程中,分析是最重要的一个环节,如果缺少这一步,会降低统计工作的作用;准确的说,没有统计分析,统计的工作就没有活力、没有发展,也就没有统计工作的意义。
采用统计分析方法进行研究,必须遵循以下几个统计学基本特征:(1)科学性;(2)直观性;(3)可重复性
统计分析除了基础的统计分析外,还包含了高级统计的知识。高级统计一般包括:回归分析、聚类分析、时间序列、生存分析、判别分析、主成分分析、因子分析、协整分析、联立方程、面板数据模型等统计分析方法。这些高级统计分析不仅包含基础的变量统计信息,还能用于对数据的分类、聚类、回归及预测。可以说高级统计分析部分应用的范围更广、使用频率更高、实际解决问题的能力更强。
统计分析方法很多,但基本方法是定量分析。然而仅仅定量分析还是不足以解决问题,所以应遵循一定的分析技巧,统计分析技巧可以按照“定性—定量—定性”的顺序,巧妙的将定量分析和定性分析结合。
1.1.算法摘要
主成分分析(principal components analysis ,PCA)也称主分量分析,旨在利用降维的思想,将多指标转化为少数几个综合指标。在统计学中,主成分分析的本质就是一种简化数据集的技术,它借助于一个正交变换,将数据变换到一个新的坐标系中,同时这些变换后的变量都是不相关的;但这些不相关的综合变量,能够尽可能多的反映原来变量的信息,使得研究复杂问题时能够更容易抓住主要矛盾。
主成分分析设法将原来众多具有相关性的指标,重新组合成一组无相关性的综合指标,用来代替原来指标。通常是将原有指标作线性组合构成新的综合指标;比如选取第一个原指标的线性组合F1,如果Var(F1)越大,表示这个综合指标包含越多信息,所以最大方差的综合指标就称为第一主成分;同时如果第一主成分不能完全反映原数据的信息,可重新计算第二主成分,方法与选取第一主成分一样,取方差最大的线性组合,但F1已有的信息就不需要重复的出现在F2中,即Cov(F1,F2)=0,所以依次类推,可计算所有满足的主成分。
1.2.算法原理
主成分分析算法要求数据无缺损,所以将有缺失值行都去除;输入数据矩阵,并赋予相应的权重;计算相关系数矩阵或协方差矩阵;计算数据矩阵的特征根和特征向量;选取特定的特征根和特征向量;计算因子载荷矩阵;计算数据矩阵的标准化得分;计算主成分。具体步骤如下:
1)计算相关系数矩阵和协方差矩阵:
叉积: ,
,
相关系数矩阵: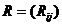 :
: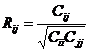
协方差矩阵: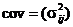 :
: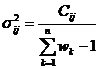
其中Z是数据,w是相应的权重。
2)计算相关系数矩阵或者协方差矩阵的特征根与特征向量:
 ,
,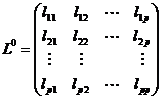
3)根据需求选取最大的前m个特征根与对应的特征向量:
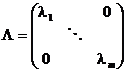 ,
,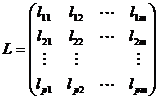
4)计算主成分贡献率及累计贡献率:
 ,
,
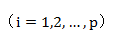
5)计算因子载荷矩阵和共性方差:
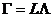 ,
,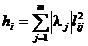
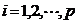
6)计算数据矩阵的列进行标准化:
列均值: ,
,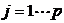
列方差: ,
,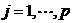
标准化元素: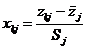 ,
,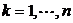 ,
,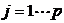
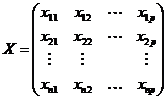
7)计算主成分:
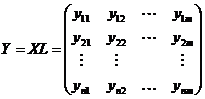
其中L为根据用户需求选取的特征根对应的特征向量。
二算法背景主成分分析由皮尔逊在1901年首先引入,当时只针对非随机变量讨论,后来霍特林在1933年对其发展,将其推广到随机变量。
三相关应用可应用于:概述数据之间的关系;将原数据转换为互不相关数据;降低数据个数,简化多变量维度;解决回归分析中共线性问题;可用来做一组变量的综合指数等。
可分析的对象:主成分分析可分析数据的不同统计量,系统支持对变量的相关系数和协方差进行分析。
可应用的领域:商业(如市场细分)、医学药理分析、化学分析、生物(如农作物生长的影响因素分析)、社会学、地质分析等。
四参考资料1.维基百科;
2.百度;
3.MBA智库百科(http://wiki.mbalib.com/)
4.马克威分析系统使用教程,www.tenly.com。
5.应用多元分析(第三版),王学民编著,上海财经大学出版社。
五实例示例数据为某炼钢厂在炼钢过程中,列举的可能会影响炼钢质量的一些指标,现要求对这些指标进行分析,判断哪些是影响炼钢质量的主要影响因素;同时新得到的炼钢数据应该归为哪一类别的钢?
| 铁水量 | 雾化能力 | 风压 | 风量 | 氧量 | 富氧程度 | 折合风量 | 单位耗风量 | 钒氧化率 |
| 112.5 | 187.5 | 2.7 | 7577 | 455 | 24.5 | 9852 | 87.6 | 94.1 |
| 123.1 | 295.4 | 2.7 | 5534 | 332 | 24.6 | 7194 | 58.4 | 75.4 |
| 101 | 303.3 | 2.6 | 4370 | 248 | 24 | 5610 | 55.5 | 96.7 |
| 88.5 | 280 | 2.8 | 4300 | 253 | 24.4 | 5566 | 62.9 | 78.7 |
| 124.8 | 325.6 | 2.7 | 5010 | 307 | 24.6 | 6545 | 52.4 | 77.1 |
| 122.9 | 388 | 2.9 | 4250 | 396 | 26.8 | 6230 | 50.7 | 72.2 |
| 79.9 | 435.8 | 3 | 2508 | 279 | 28 | 3902 | 48.8 | 59.4 |
| 129 | 339.5 | 2.7 | 4942 | 307 | 24.7 | 6477 | 50.2 | 81 |
| 105.2 | 287 | 2.5 | 4912 | 307 | 24.7 | 6447 | 58.6 | 82.2 |
| 110 | 350.6 | 2.8 | 3750 | 240 | 24.8 | 4950 | 47 | 67.8 |
| 80.7 | 322.8 | 2.6 | 3120 | 200 | 24.8 | 4120 | 51.2 | 70.6 |
应用主成分分析分析这些指标之间的关系,计算的结果如下所示:
特征根和累计贡献率:
| 主成分 | 特征根 | 方差贡献率% | 累计贡献率% |
| 1 | 5.4288 | 60.3205 | 60.3205 |
| 2 | 2.0144 | 22.3820 | 82.7025 |
| 3 | 1.0325 | 11.4720 | 94.1744 |
| 4 | 0.2754 | 3.0600 | 97.2344 |
| 5 | 0.2326 | 2.5842 | 99.8186 |
| 6 | 0.0145 | 0.1608 | 99.9794 |
| 7 | 0.0017 | 0.0184 | 99.9978 |
| 8 | 0.0002 | 0.0022 | 100.0000 |
| 9 | 0.0000 | 0.0000 | 100.0000 |
特征向量:
|
|
特征向量1 | 特征向量2 | 特征向量3 |
| 1 | 0.225 | 0.2592 | -0.7528 |
| 2 | -0.3903 | 0.1943 | -0.2604 |
| 3 | -0.2311 | 0.5025 | 0.2249 |
| 4 | 0.4164 | 0.1485 | -0.0339 |
| 5 | 0.2712 | 0.5326 | 0.0097 |
| 6 | -0.2808 | 0.4773 | 0.1813 |
| 7 | 0.402 | 0.2413 | -0.0256 |
| 8 | 0.3557 | 0.103 | 0.5292 |
| 9 | 0.3601 | -0.2005 | 0.0114 |
主成分载荷矩阵:
|
|
主成分1 | 主成分2 | 主成分3 |
| 铁水量 | 0.5242 | 0.2592 | 0.7649 |
| 雾化能力 | -0.9095 | 0.2757 | 0.2646 |
| 风压 | -0.5384 | 0.7132 | -0.2286 |
| 风量 | 0.9703 | 0.2107 | 0.0344 |
| 氧量 | 0.6319 | 0.7559 | -0.0098 |
| 富氧程度 | -0.6543 | 0.6775 | -0.1842 |
| 折合风量 | 0.9367 | 0.3424 | 0.0260 |
| 单位耗风量 | 0.8289 | 0.1461 | -0.5377 |
| 钒氧化率 | 0.8390 | -0.2846 | -0.0116 |
从特征根及方差贡献率可以得到:前三个主成分基本上可以概括该数据的所以信息,所以本例中可以选取三个主成分。
同时前三个主成分对应的特征向量也给出了。这些特征向量其实就是主成分用标准化变量表示的系数,即:
Y1=0.225*X1-0.3903*X2+……;Y2=0.2592*X1+0.1943*X2+……;
Y3=-0.7528*X1-0.2604*X2+….
其中标准化变量Xi与原变量xi的关系:Xi=(xi-均值)/Si。
主成分载荷矩阵表示:在各主成分中,原始变量对主成分影响大小情况;其中系数的绝对值越大,表示受影响就越大。例如,在主成分1中,雾化能力、风量、折合风量等对主成分1影响最大,符号的正负表示起促进作用还是抑制作用。
六输入输出输入变量类型:要求数值型变量;如整型、浮点型(注:参与主成分分析的变量要求至少2个;数据要求没有缺损。)
输出结果:得到影响结果的互不相关的变量、特征根和累计贡献率等。
七相关条目方差贡献率、协方差矩阵、主成分载荷
八优缺点8.1.优点
1)可消除评估指标之间的相关影响;因为主成分分析法在对原始数据指标变量进行变换后形成了彼此相互独立的主成分,而且实践证明指标间相关程度越高,主成分分析效果越好。
2)可减少指标选择的工作量,对于其他评估方法,由于难以消除评估指标间的相关影响,所以选择指标时要花费不少精力,而主成分分析法由于可以消除这种相关影响,所以在指标选择上相对容易些。
3)主成分分析中各主成分是按方差大小依次排列顺序的,在分析问题时,可以舍弃一部分主成分,只取前面方差较大的几个主成分来代表原变 量,从而减少了计算工作量。用主成分分析法作综合评估时,由于选择的原则是累计贡献率≥85%,不至于因为节省了工作量却把关键指标漏掉而影响评估结果。
8.2.缺点:
1)在主成分分析中,我们首先应保证所提取的前几个主成分的累计贡献率达到一个较高的水平(即变量降维后的信息量须保持在一个较高水平上),其次对这些被提取的主成分必须都能够给出符合实际背景和意义的解释(否则主成分将空有信息量而无实际含义)。
2)主成分的解释其含义一般多少带有点模糊性,不像原始变量的含义那么清楚、确切,这是变量降维过程中不得不付出的代价。因此,提取的主成分个数m通常应明显小于原始变量个数p(除非p本身较小),否则维数降低的“利”可能抵不过主成分含义不如原始变量清楚的“弊”。
3)当主成分的因子负荷的符号有正有负时,综合评价函数意义就不明确。