
非参数检验是指在总体分布形式未知情况下,可以通过对样本进行检验,以考察总体的分布形式。这是因为在现实问题中,有时不能知道总体服从什么类型的分布,而按照经验或某种理论我们不能对总体进行一些假设,或仅能作一些非常一般性(例如连续分布、对称分布等)的假设,这时候仍用参数检验,其推断出来的结果显然不可信,甚至有可能是错的。所以,必须先对总体的分布做一定的检验,然后才能用参数检验对总体进行推断。
非参数检验的方法,对样本是否来自于正态总体不做严格的限制,而且计算简单;一般非参数检验包含卡方检验、符号检验、秩和检验等检验方法。
非参数检验适用于以下类型的资料:(1)等级资料(有序分类资料)。如疗效按治愈、显效、有效、无效分组的资料;(2)偏态分布资料。当观察值呈偏态或极度偏态分布,而又未经变量变换或虽经变换但仍未达到正态或近似正态分布;(3)分布不明的资料。如新指标分布形态不明,小样本,但不趋向正态分布资料;(4)各组方差明显不齐,且不易变换达到齐性;(5)组内个别观察值偏离过大的资料。(6)开口分组资料。数据分组某一端或两端无明确数值的资料,只给出一个下限或上限,而没有具体数值,如大于等于60岁等。
非参数检验的特点:(1)主要优点是不受总体分布的限制,适用范围广;(2)对适宜用参数统计检验的资料,若用非参数检验处理,会损失部分信息,降低统计检验效率,即犯第二类错误的概率比参数检验大;(3)对于适合参数统计检验条件的资料或变量变换后适合于参数统计检验,最好使用参数检验。当资料不具备用参数检验的条件时,非参数检验是很有效的分析方法。
1.1 算法摘要
独立样本检验包含了两个及两个以上的独立样本检验,目的是为了检验样本是否来自于同一总体;通过检验两个及多个独立样本的均值、中位数等进行检验,来分析它们是否来自相同的分布。其中独立样本是指在一个总体中随机抽样对在另一个总体中随机抽样没有影响的情况下所获得的样本。
1.2 算法原理
1.2.1 两个独立样本检验
对两个独立样本的检验方法,常用的包括:曼-惠特尼U(Mann-Whitney U)检验、沃尔德-沃尔佛威茨(Wald-Wolfowitz)检验、柯尔莫哥洛夫-斯米尔诺夫(Kolmogorov-Smirnov)检验和莫斯(Moses)检验。
1、曼-惠特尼U检验的计算过程
(1)统计两个样本的频数,把两个样本混合并编秩,然后把每组样本的秩相加,求出每组样本的秩和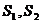 和平均秩
和平均秩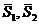 ,修正值
,修正值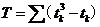 ,把第
,把第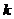 个同秩的频数记为
个同秩的频数记为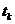 ;
;
(2)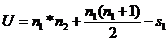 ,如果U>n1*n2/2,U= n1*n2-U
,如果U>n1*n2/2,U= n1*n2-U
W=平均秩小的所对应的秩和

其中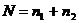 ;
;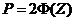 ;
;
2、科尔莫哥罗夫-斯米尔若夫检验的计算过程
(1)统计两个样本的频数,并计算两个样本的经验分布函数F1(x)和F2(x),把两个样本混合并按照升序排列,得到新的序列Zi;
(2)计算差值序列、正差、负差、绝对差
Di=F1(Zi)-F2(Zi);D+=max(Di)其中Di>0;D-=min(Di)其中Di<0;
D
=max(D+,-D-)
(3)同时Z和P的计算公式为
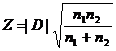 ;
;

3、莫斯检验的计算过程
分别统计两个样本的频数,并把两个样本的数据混合编秩,并对第一个样本求出截断前后样本的秩跨度S1和S2以及相应的显著性水平P1和P2,截断长度h。
4、沃尔德-沃尔佛威茨检验的计算过程
分别统计两个样本的频数,将两样本混合按升序排列,对新序列的数据根据来自的样本计算游程,对于两个样本中共有的元素,枚举所有的可能游程计算相应的游程数,得到最大可能的游程Umax和最小可能的游程Umin;按照求解公式计算Z统计量和p值。
1.2.2 多个独立样本检验
对多个独立样本的检验方法包括:克拉夏尔-瓦里斯(Kruskal-Wallis)检验和中位数(Median)检验法。
1、克拉夏尔-瓦里斯检验的计算过程
(1)统计各列的长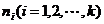 ;
;
(2)把所有列的数据混合并编秩,计算各列的秩和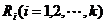 、修正值
、修正值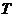 及平均秩;
及平均秩;
(3) ,其中
,其中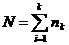 ;
;
自由度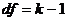 ;
;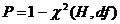 其中
其中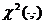 为卡方分布函数
为卡方分布函数
2、中位数检验的计算过程
(1)统计各列的样本数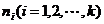 ,把所有列的样本混合并按升序排列,得到一个新序列
,把所有列的样本混合并按升序排列,得到一个新序列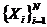 ,
,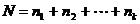 ;
;
(2)求出该序列的中间值 ,
,
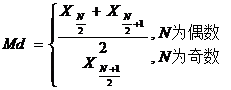 ;
;
(3)根据 的值对各列数据分类统计频数,得到一个
的值对各列数据分类统计频数,得到一个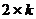 矩阵
矩阵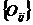 ;
;
(4)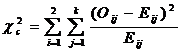 其中
其中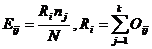 ;
;
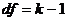 ;
;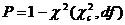 ,其中
,其中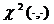 为卡方分布函数。
为卡方分布函数。
独立样本的检验主要用来检验两个独立样本是否来自同一个总体。可以应用于任何领域的数值型数据。
四参考资料1 独立样本检验—百度百科
2 马克威分析系统使用教程,http://www.tenly.com
五实例1、两个独立样本检验
示例数据为某工厂用两种不同的工艺生产同一种灯泡,技术人员试图通过比较灯泡的使用寿命来比较两种工艺的优劣,分析工艺是否对灯泡的使用寿命产生显著性差异?
| 工艺类型 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|
| 寿命 | 675 | 682 | 692 | 679 | 669 | 661 | 693 |
|
| 工艺类型 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 寿命 | 662 | 649 | 672 | 663 | 650 | 651 | 646 | 652 |
以曼-惠特尼U检验对该例子进行推断,经计算后得到的结果如下所示:
|
|
曼-惠特尼U | 威尔科克森W | Z | 渐近显著性(双侧) |
| 寿命 | 4.0000 | 40 | -2.7775 | 0.0055 |
从计算的显著性水平P=0.0055<0.05,即拒绝原假设,认为两种工艺对灯泡的使用寿命有显著性的差异。
2、多个独立样本检验
示例数据为四个城市的初三学生物理成绩,分析各城市初中毕业物理成绩是否存在显著性差异?
| 城市 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 |
| 成绩 | 79 | 75 | 78 | 76 | 72 | 72 | 71 | 74 | 74 | 73 |
| 城市 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 |
| 成绩 | 76 | 78 | 78 | 77 | 75 | 70 | 72 | 71 | 71 | 69 |
以克拉夏尔-瓦里斯检验对该例子进行推断,经计算后得到的结果如下所示:
|
|
卡方值 | 自由度 | 渐近显著性 |
| 物理成绩 | 13.8996 | 3 | 0.0030 |
从计算的显著性水平P=0.003<0.05,即拒绝原假设,认为四个城市初中毕业班物理成绩存在显著性差异。
六输入输出输入变量表数据类型:整型、浮点型、布尔型
输入数据尺度:标量型、名义型、有序型
输出结果:计算出数据的显著性水平,并与默认的显著性水平比较
七相关条目独立样本、假设检验、Z统计量、置信水平
八优缺点优点:能够分析独立样本之间的假设检验,以样本数据推断总体数据的分布