非参数检验是指在总体分布形式未知情况下，可以通过对样本进行检验，以考察总体的分布形式。这是因为在现实问题中，有时不能知道总体服从什么类型的分布，而按照经验或某种理论我们不能对总体进行一些假设，或仅能作一些非常一般性（例如连续分布、对称分布等）的假设，这时候仍用参数检验，其推断出来的结果显然不可信，甚至有可能是错的。所以，必须先对总体的分布做一定的检验，然后才能用参数检验对总体进行推断。
非参数检验的方法，对样本是否来自于正态总体不做严格的限制，而且计算简单；一般非参数检验包含卡方检验、符号检验、秩和检验等检验方法。
非参数检验适用于以下类型的资料：（1）等级资料（有序分类资料）。如疗效按治愈、显效、有效、无效分组的资料；（2）偏态分布资料。当观察值呈偏态或极度偏态分布，而又未经变量变换或虽经变换但仍未达到正态或近似正态分布；（3）分布不明的资料。如新指标分布形态不明，小样本，但不趋向正态分布资料；（4）各组方差明显不齐，且不易变换达到齐性；（5）组内个别观察值偏离过大的资料。（6）开口分组资料。数据分组某一端或两端无明确数值的资料，只给出一个下限或上限，而没有具体数值，如大于等于60岁等。
非参数检验的特点：（1）主要优点是不受总体分布的限制，适用范围广；（2）对适宜用参数统计检验的资料，若用非参数检验处理，会损失部分信息，降低统计检验效率，即犯第二类错误的概率比参数检验大；（3）对于适合参数统计检验条件的资料或变量变换后适合于参数统计检验，最好使用参数检验。当资料不具备用参数检验的条件时，非参数检验是很有效的分析方法。
1.1 算法摘要
符号检验法是通过对两个相关样本的每对数据之差的符号进行检验，从而比较两个样本的显著性。具体来说，若两个样本差异不显著，则正差值和负差值的个数应大致各占一半。
根据符号检验判断是否显著性差异时，需要查表找出相应参数下的临界值。但特别应注意的是在某一显著性水平下，实得的r值大于表中r的临界值是，表示差异不显著，这点与参数检验时统计量和临界值的判断结果不同。
1.2 算法原理
符号检验的过程及步骤：
设两个总体X1,X2，它们的分布皆未知，以f1(x)和f2(x)分别表示两总体的概率密度。我们要检验f1(x)= f2(x)是否成立。于是，建立原假设与备择假设为：
H0:f1(x)=f2(x), H1: f1(x)≠f2(x)
为此对两个总体分别独立地抽取m个元素，即得到m对数据：
(a1,b1),(a2,b2),…,(am,bm)
如果f1(x)=f2(x)假设成立，那么ai>bi或ai<bi(i=1,2,…,m)应该有相同的概率(1/2),且样本ai>bi与ai<bi的个数差异不应很大。
令ai>bi的事件为yi,其取值为1，0
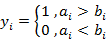
于是
y=y1+y2+...+ym
服从二项分布。根据二项分布计算出了比较ai>bi或ai<bi差异的临界值Sa(Ｎ)；该临界值须经过查表得到数据。
鉴于上述思想，我们给出符号检验的方法步骤：
（1）将两总体的样本数据进行比较，且
ai>bi记为“+”,“+”的个数记为N+
ai<bi记为“-”,“-”的个数记为N-
ai=bi记为“0”,“0”的个数记为N0
（2）求出N：
N=N++Ｎ-
（3）在显著水平α下，根据Ｎ值查符号检验表得其临界值Sa(Ｎ)；
（4）判别显著性
若S0=min{Ｎ+,Ｎ-}<Sa(Ｎ),则拒绝H0,接受H1；认为f1(x)与f2(x)有显著差异。
若S0=min{Ｎ+,Ｎ-}>Sa(Ｎ)，则接受H0，认为f1(x)与f2(x)无显著差异。
三相关应用符号检验与参数检验中相关样本显著性t检验相对应，当资料不满足参数检验条件时，可采用符号检验两个相关样本的差异显著性。
小样本（N<25）时的检验方法，小样本是属于二项分布的问题，直接用符号检验的方式得出结果；大样本（N>25）时的检验方法，二项分布近似于正态分布，因此可以用Z比率作为检验统计量。
检验的公式为：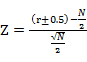
，其中r为N+或N-的数值，N为N+和N-的和。当r>N/2时用r-0.5；当r<N/2时用r+0.5。
1 符号检验—MBA智库百科
2 马克威分析系统使用教程，http://www.tenly.com
五实例1、小样本数据的符号检验方法
示例数据为研究员将三岁儿童经配对而成的实验组进行特殊试验教学，对照组不进行此种教学；问特殊教学是否有显著性效果？
| 配对 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 实验组 | 18 | 20 | 26 | 14 | 25 | 25 | 21 | 12 | 14 | 17 | 20 | 19 |
| 对照组 | 14 | 20 | 23 | 12 | 29 | 18 | 21 | 10 | 16 | 13 | 17 | 25 |
| 差数符号 | + | 0 | + | + | - | + | 0 | + | - | + | + | - |
检验步骤：
（1）建立假设：
原假设H0：特殊教学无显著效果；备择假设H1：特殊教学有显著效果
（2）求差数并记下符号：如表中的结果可知“+”和“-”的个数分别为
N+=7，N-=3；则N=N++N-=7+3=10；其中较小的记为r=3。
（3）统计决断：根据N=10及r=3；查表在显著性水平为0.05条件下，得到的数值为：X0.05=1，由于符号检验表是单侧检验表，所以在进行双侧检验时，其显著性水平应乘以2，所以r=3>2，接受原假设H0，认为特殊教学无显著性效果。
2、大样本数据的符号检验方法
示例数据为对30名幼儿园教师进行手工技能培训，培训前后的数据如下，分析培训前后的两次测验结果差异是否显著？
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 培训前 | 70 | 65 | 86 | 71 | 61 | 90 | 64 | 70 | 94 | 69 | 55 | 60 | 91 | 85 | 82 |
| 培训后 | 76 | 66 | 79 | 79 | 65 | 87 | 73 | 85 | 92 | 74 | 53 | 64 | 96 | 82 | 86 |
| 差数符号 | - | - | + | - | - | + | - | - | + | - | + | - | - | + | - |
| 序号 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 培训前 | 88 | 74 | 66 | 89 | 67 | 62 | 83 | 86 | 84 | 64 | 72 | 74 | 58 | 60 | 94 |
| 培训后 | 90 | 79 | 62 | 90 | 78 | 70 | 77 | 93 | 89 | 63 | 88 | 80 | 60 | 70 | 89 |
| 差数符号 | - | - | + | - | - | - | + | - | - | + | - | - | - | - | + |
检验步骤：
（1）建立假设：
原假设H0：手工技能培训无显著效果；
备择假设H1：手工技能培训有显著效果
（2）求差数并记符号：符号如表中所示，其中“＋”和“－”的个数分别为N+=9，N-=21；Ｎ＝Ｎ＋＋Ｎ－＝30；r=min{N+，N-}=9。
由于样本容量较大，则可使用Z作为统计量公式计算；并且r=9<N/2=15，用r+0.5计算，得到：
（3）统计决断：因为Z的绝对值2.372>1.96，所以在0.05的显著性水平上拒绝原假设，接受备择假设。认为手工技能培训有显著性效果。
六输入输出输入变量变量表数据类型：整型、浮点型、布尔型
输入数据尺度：标量型、名义型、有序型
输出结果：取值的实际频数、观察比率、检验概率和显著性水平
七相关条目非参数检验、秩和检验、卡方检验、Z统计量
八优缺点优点：不需要对所要检验的两个总体的分布形态做任何假定，并且计算简单。
缺点：只考虑符号，不考察差数的大小，因而会失去样本所提供的一部分信息；而且必须在数据成对时使用。对于同一个样本数据，采用符号检验的精确度，只相当于卡方检验的60%，因此除了小样本，一般不使用符号检验。
