
统计,顾名思义即将信息统括起来进行计算的意思,它是对数据进行定量处理的理论与技术。统计分析,常指对收集到的有关数据资料进行整理归类并进行解释的过程。在整个统计分析的过程中,分析是最重要的一个环节,如果缺少这一步,会降低统计工作的作用。准确的说,没有统计分析,统计的工作就没有活力、没有发展,也就没有统计工作的意义。
采用统计分析方法进行研究,必须遵循以下几个统计学基本特征:(1)科学性;(2)直观性;(3)可重复性
统计分析方法按功能标准进行划分,可分为描述统计和推断统计。
描述统计是将数据整理、归纳,并将这种关系以图表形式展现;主要涉及数据的集中趋势、离散程度和相关强度,最常用的指标有均值、标准差和相关系数等统计量。最常用的算法有均值分析,频率分析,描述统计等。
推断统计是指用概率形式来决断数据之间是否存在某种关系及用样本统计值来推测总体特征的一种重要的统计方法;推断统计包括总体分布已知的总体参数估计和假设检验,总体分布未知的非参数检验。最常用的参数检验方法有Z检验、T检验,非参数检验的方法包括卡方检验、符号检验、秩和检验等。
统计分析方法很多,但基本方法是定量分析。然而仅仅定量分析还是不足以解决问题,所以应遵循一定的分析技巧,统计分析技巧可以按照“定性-定量-定性”的顺序,巧妙的将定量分析和定性分析结合。
频率分析对变量观测数据按组进行归纳整理,对变量的极差、标准差、偏度、峰度等统计量进行计算;同时也对变量的频率、百分比、累积百分比进行统计分析,得到变量取不同值时的频数分析表,形成对数据的数量特征和观测量分布状况的总体认识。
频率分析在平时也用的非常多,在得到变量取不同值时的频数分析,能对数据的数量特征和观测分布状况得到初步认识。其中的一些基本统计量的计算公式为:
频率:

其中j=1,2,……,N;ki的取值为1当Xi=Xj时成立,其他为0
权重:
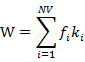
当Xi缺失时,ki为0,其他为1
均值: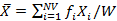
方差: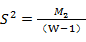 ,其中
,其中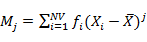 ,j=2,3,4
,j=2,3,4
标准差: ;均值标准误差:
;均值标准误差: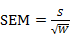
偏度:
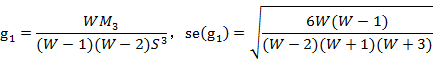
峰度:
 三相关应用
三相关应用
频率分析应用领域无明显的限制。但频率分析在数学、物理学、信号处理及密码学中应用的比较多。比如在密码学中,频率分析指的是研究字母或者字母组合在文本中出现的频率,应用频率分析,可以破解古典密码。
四参考资料1 贾俊平编著,统计学,4版,北京:中国人民大学出版社,2011
2 陈希孺.概率论与数理统计.合肥:中国科学技术大学出版社,1992
3 盛骤,谢式千,潘承毅:概率论与数理统计,第四版,北京:高等教育出版社,2008
4 何晓群编著,现代统计分析方法与应用.第二版,中国人民大学出版社2007
5 马克威分析系统使用教程,http://www.tenly.com
五实例示例数据为抽取的某小学五年级20名学生的期中考试英语成绩及学生的身高、体重数据。以频率分析了解学生分数、身高、体重的基本特征(单位:cm,kg)
| 学号 | 分数 | 身高 | 体重 |
| 1 | 81 | 146 | 41 |
| 2 | 80 | 145 | 40 |
| 3 | 73 | 138 | 33 |
| 4 | 72 | 137 | 32 |
| 5 | 67 | 132 | 35 |
| 6 | 92 | 157 | 52 |
| 7 | 88 | 153 | 48 |
| 8 | 87 | 152 | 47 |
| 9 | 86 | 151 | 46 |
| 10 | 84 | 149 | 44 |
| 11 | 83 | 148 | 43 |
| 12 | 83 | 148 | 43 |
| 13 | 83 | 148 | 43 |
| 14 | 81 | 146 | 41 |
| 15 | 80 | 145 | 40 |
| 16 | 80 | 145 | 40 |
| 17 | 78 | 143 | 38 |
| 18 | 75 | 140 | 35 |
| 19 | 74 | 139 | 34 |
| 20 | 72 | 137 | 32 |
计算学生分数、身高及体重频率分析的部分统计结果:
| 类别 | 极差 | 标准差 | 方差 | 偏度 | 峰度 |
| 分数 | 25 | 6.278 | 39.42 | -0.202 | -0.288 |
| 身高 | 24.4 | 6.217 | 38.66 | -0.239 | -0.388 |
输入变量类型:整型、浮点型;
输入数据尺度:标量型、有序型、名义型;
输出结果:描述中心趋势统计量、描述离中趋势统计量、描述分布的统计量。
七相关条目统计量、百分比、比例
八优缺点优点:频率分析应用范围广泛,可得到变量取不同值时的频数分析,能对数据的数量特征和观测分布状况有一个清晰的了解。