
假设检验是用来判断样本与样本,样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。其基本原理是先对总体的特征作某种假设,然后通过抽样研究的统计推理,对此假设应该被拒绝还是接受作推断。
假设检验又分为对已知分布的参数检验和对未知分布的非参数检验。参数检验要利用到总体的信息,如总体分布、总体的一些特征和方差;以总体分布和样本信息对总体参数作推断。
参数检验可以分为:以单样本数据的均值推断总体的均值;单样本数据的方差推断总体的方差;以相互独立的双样本数据来推断样本是否来自于同均值或同方差的总体;样本数据的比例检验验证总体数据的比例。
假设检验的基本思想:小概率原理。如果对总体的某种假设是真实的,那么不利于或者不能支持这一假设的事件A(小概率事件)在一次试验中几乎不可能发生的,要是在一次试验中A发生了,就有理由怀疑该假设的真实性,拒绝这一假设。
1.1算法摘要
样本均值检验又分为单样本均值检验和双样本均值检验。单样本均值检验通过样本数据检验变量均值与给定数值之间是否存在显著性差异,亦即检验一个样本是否来自于具有指定均值的总体。双样本均值检验依据来自于两个总体的独立样本,检验两个总体均值是否有显著性差异。
对于来自单个或两个正态总体的样本(样本之间相互独立),按照方差是否已知使用不同的检验方法:方差已知时,采用常见的U检验,此时检验统计量服从标准正态分布;方差未知时,检验统计量服从t分布,采用 t检验。
1.2算法原理
1.2.1 参数检验的基本思想
小概率原理:小概率事件在一次试验中是几乎不可能发生的,假若在一次试验中事件 事实上发生了。那只能认为事件 不是来自我们假设的总体,也就是认为我们对总体所做的假设不正确。
1.2.2 参数检验的含义
参数显著性检验即用于实验处理组与对照组或两种不同处理的效应之间是否有差异,以及这种差异是否显著的方法。常把一个要检验的假设记作H0,称为原假设(或零假设) (null hypothesis) ,与H0对立的假设记作H1,称为备择假设(alternative hypothesis) 。
⑴ 在原假设为真时,决定放弃原假设,称为第一类错误,其出现的概率通常记作α;
⑵ 在原假设不真时,决定接受原假设,称为第二类错误,其出现的概率通常记作β。
通常只限定犯第一类错误的最大概率α,不考虑犯第二类错误的概率β。这样的假设检验又称为显著性检验,概率α称为显著性水平。最常用的α值为0.01、0.05、0.10等。一般情况下,根据研究的问题,如果选择弃真错误则损失比较大,为减少这类错误,α取值小些,反之,α取值大些。
1.2.3 总体均值为定值的均值检验
总体均值的显著性检验可有双尾、左单尾、右单尾三种不同的情况。下面就总体分布的不同情况,总体方差是否已知的不同情况以及样本大小的不同情况分别介绍检验统计量和检验规则。
(1)总体为正态分布,总体方差已知,样本不论大小
对于假设:H0:μ = μ0,在H0成立的前提下,有检验统计量
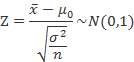
如果规定显著性水平为在双尾,左单尾,右单尾三种不同情形下,拒绝域分别为:① 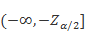 和
和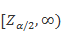 ;②
;②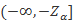 ;③
;③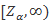 。
。
(2)总体分布未知,总体方差已知,大样本
对于假设H0:μ = μ0,在H0成立的前提下,如果样本足够大(n≥30),近似地有检验统计量
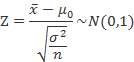
如果规定显著性水平为a,在双尾,左单尾,右单尾三种不同情形下,拒绝域分别为: ① 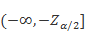 和
和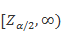 ;②
;②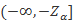 ;③
;③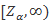 。
。
(3)总体为正态分布,总体方差未知,小样本
对于假设H0:μ = μ0,在H0成立的前提下,有检验统计量
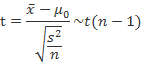
如果规定显著性水平为a,在双尾,左单尾,右单尾三种不同情形下,拒绝域分别为:①  和
和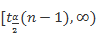 ;②
;②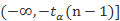 ;③
;③ 。
。
(4)总体分布未知,总体方差未知,大样本
对于假设H0:μ = μ0,在H0成立的前提下,如果总体偏斜适度,且样本足够大,近似地有检验统计量
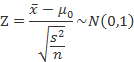
如果规定显著性水平为a,在双尾,左单尾,右单尾三种不同情形下,拒绝域分别为:① 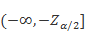 和
和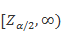 ;②
;②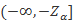 ;③
;③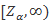 。
。
样本均值的检验用来推断总体特征。可以对任何领域的数值型数据进行检验。
例如对采购原材料的验证,我们抽样所得到的数据在目标值两边波动,有时波动范围很大,这时要判断这些原材料是否达到了规定的要求,再比如,做了两组实验,要比较这两组实验的合格率有无显著性变化等问题;所以针对这类需要判断样本数据的均值是否与总体的常数相一致。
四参考资料1维基百科
2百度
3马克威分析系统使用教程,www.tenly.com
4《应用多元分析(第三版)》,王学民编著,上海财经大学出版社
5《多元统计分析》,张润楚,科学出版社2006年版
五实例1、单样本均值检验过程
示例数据为某公司部门员工得到工龄,分析员工的平均年龄是否为10年,并分析其差异性。
| 编号 | 工龄 |
| 1 | 16 |
| 2 | 8 |
| 3 | 7 |
| 4 | 16 |
| 5 | 15 |
| 6 | 14 |
| 7 | 12 |
| 8 | 12 |
| 9 | 13 |
| 10 | 10 |
| 11 | 14 |
| 12 | 12 |
| 13 | 8 |
对该问题的求解过程:
首先提出两个假设,一个为原假设H0:μ = 10,备择假设为H1:μ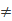 10,取置信水平为0.95,则经过计算得到:
10,取置信水平为0.95,则经过计算得到:
| T统计量 | 自由度 | P值 | 均值差上限 | 均值差下限 |
| 2.463 | 12 | 0.0299 | 0.2397 | 3.9142 |
从得到的结果来看:P=0.0299<0.05,认为拒绝原假设,而选择备择假设,即该公司部门员工的平均工龄不等于10年。
2、独立的双样本均值检验
示例数据为某公司部门员工得到工龄,分析两组员工的平均年龄是否有显著性的差异。
| 编号 | 员工组1 | 员工组2 |
| 1 | 16 | 2 |
| 2 | 8 | 5 |
| 3 | 7 | 7 |
| 4 | 16 | 8 |
| 5 | 15 | 9 |
| 6 | 14 | 15 |
| 7 | 12 | 13 |
| 8 | 12 | 11 |
| 9 | 13 | 12 |
| 10 | 10 | 13 |
| 11 | 14 | 14 |
| 12 | 12 | 11 |
| 13 | 8 | 10 |
首先提出两个假设,一个为原假设H0:μ1 =μ2,备择假设为H1:μ1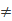 μ2,取置信水平为0.95,同时假设两个样本的方差是相等的,则经过计算得到:
μ2,取置信水平为0.95,同时假设两个样本的方差是相等的,则经过计算得到:
| T统计量 | 自由度 | P值 | 均值的差值 | 均值标准误差 |
| 1.5532 | 24 | 0.1335 | 2.0769 | 1.3371 |
从结果的P>0.05,则可认为接受原假设,即两组员工的工龄无显著性差别。
六输入输出输入变量类型:整型、浮点型
输入数据尺度:标量型、名义型、有序型
输出结果:统计表和检验结果
七相关条目假设检验、小概率事件、Z检验、T检验、抽样
八优缺点优点:检验效率高
缺点:总体分布非正态,且无法通过适当的变量变换达到正态分布,或者分布类型未知,则不能使用;精确测量后才有可能计算参数统计量,不可用非精确测量的数据;对于分类样本,作用有限。