
一 定义:时间序列是指将某一现象所发生的数量变化,依时间的先后顺序排列,以揭示随着时间的推移,这一现象的发展规律,从而用以预测现象发展的方向及其数量。
二 时间序列分类:水平型时间序列、季节型时间序列、循环型时间序列、直线趋势型时间序列和曲线趋势型时间序列。
1)水平型:又称为稳定型时间序列或平稳型时间序列。这是因为这种数据走势无倾向性,不增不减,总是在某一个水平上下波动,同时这种波动也是无规律性。如日用必需品的销售量,某耐用消费品的合格率、返修率等等。
2)季节型:序列的走势按时间发生周期性的变化,即在某段时间后序列值逐步向上,到顶峰后逐步向下,后来又逐步向上,周而复始。如与季节气候有关的季节型商品的销售量等。
3)循环型:循环型时间数列的走势也呈周期性变化,但他不是在一个不变的时间间隔中反复出现,且每一周期长度一般都有若干年。通常呈循环型时间数列的有期货价格、商业周期等等。
4)直线趋势型:序列显示出一定的倾向性,即在一段时间内呈现逐步增加或逐步减少的趋势。如某段时间的人均收入、商品的销售量等等。
5)曲线趋势型:序列走势也具有倾向性,会逐渐转向,包括顺转和逆转,但不发生周期性的变化,时间序列后序值增加或减少的幅度会逐渐扩大或缩小。如某商品从进入市场到被市场淘汰的销售量变化等。
三 时间序列组成成分:一个典型的时间序列可分为四个部分:趋势、季节、周期和随机波动。趋势是数据在一段时间的逐渐向上或向下的波动。季节是数据自身经过一定周期的天数,周数,月数或季度数的不断重复性。周期为数据每隔几年重复发生的时间序列形式,他们一般与经济周期相关,并对短期经营分析与计划起重要作用。随机波动是由偶然、非经常性原因引起的数据变动,它们没有可识别的形式。
四 时间序列分析方法:时间序列分析力求以历史数据为基础预测未来,其中包含很多种预测模型:移动平均法、指数平滑法、ARIMA法、季节解构法等。在实际的应用中选择哪种模型预测取决于:预测的时间范围;能否获得相关数据;所需的预测精度;预测预算的规模;合格的预测人员等。
1.1 算法摘要
ARIMA模型(Autoregressive Integrated Moving Average Model)又称为自回归移动平均模型,是时间序列分析中最常用的模型之一,它是通过自身的过去值、过去误差、其它时间序列的当前值和过去值的线性组合来预测未来响应的时间序列。
ARIMA(p,d,q)中,AR表示的是自回归,p为自回归项数;MA表示的是移动平均,q为移动平均项数;d为使时间序列成为平稳序列所做的差分次数。所以ARIMA模型可分为3种:1)自回归模型(简称AR模型);2)移动平均模型(简称MA模型);3)自回归移动平均混合模型(简称ARIMA模型)
1.2 算法原理
ARIMA模型又称为差分自回归移动平均模型,主要由自回归、差分和移动平均构成。而时间序列主要用来预测,它的基本思路为:设时间序列(或随机过程)的任意元素yt与其前期元素(yt-1、yt-2等)之间存在着某种关联,这样我们就可以根据时间序列的以往观测值来预测其在未来的取值。
ARIMA模型由三部分构成,则第一部分为自回归模型。记p阶自回归过程为AR(p),指的是如下形式的随机过程:
Yt=a1Yt-1+a2Yt-2+…+apYt-p+ut
其中a1,a2,…,ap是p个待求参数;p是滞后期限的数目;ut为白噪声即满足经典计量经济模型的随机误差。
一般的,经济系统中任何经济变量的时间序列都可以用上述自回归过程来描述。但实际问题的参数是很多的,为了减少模型之中的参数,可用移动平均过程MA(q)来表示一系列随机过程。考虑下列形式的自回归过程:
Yt = aYt-1+a2Yt-2+…+ apYt-p+…+ut
记过计算后得到表达式为:Yt=ut+aYt-1.这种情况描述的是q=1的情况,依次类推,一般的,q阶移动平均过程MA(q)表示的就是如下形式的随机过程:
Yt =ut+(b1ut-1)+(b2ut-2)+(b3ut-3)+…+(bqut-q)
所以自回归移动平均模型就是设法将自回归过程AR和移动平均过程MA结合起来,共同模拟产生既有时间序列样本数据的随机过程。然而,一般的时间序列都是不平稳的,而ARIMA算法仅可以对平稳的时间序列进行计算,所以引入差分变换,将非平稳序列转换为平稳的序列。其中ARMA(p,q)可理解为当d=0时ARIMA(p,d,q)的特例。
二算法背景上个世纪70年代,ARIMA算法由博克斯和詹金斯首先提出来,这种算法主要应用于时间经济序列的预测方法,所以又称博克斯-詹金斯法。
三相关应用ARIMA模型对等间距时间序列进行观察、研究,找寻它变化发展的规律,预测它将来的走势;该模型是分析和预测等距序列数据、转移函数数据、干预数据的一种方法。
在经济预测中既考虑了经济现象在时间序列的依存性,同时考虑了随机波动的干扰性,对经济运行短期趋势的预测准确率较高,具有广泛的应用。该模型要求时间序列必须满足平稳性的条件,所以运用的流程如下:
1)根据时间序列的散点图、自相关函数和偏自相关函数图识别其平稳性。
2)对非平稳的时间序列数据进行平稳化处理。直到处理后的自相关函数和偏自相关函数的数值不显著;
3)根据所识别出来的特征建立相应的时间序列模型。平稳化处理后,若偏自相关函数是截尾的,而自相关函数是拖尾的,则建立AR模型;若偏自相关函数是拖尾的,而自相关函数是截尾的,则建立MA模型;若偏自相关函数和自相关函数均是拖尾的,则序列适合ARMA模型;
4)参数估计,检验是否具有统计意义;
5)假设检验,判断残差序列是否为白噪声序列;
6)利用已通过检验的模型进行预测。
四参考资料1 G. E. P. Box and G. M. Jenkins.Time Series Analysis: Forecasting and Control.San Francisco:Holden Day,1976
2 Shumway R H and Stoffer D S ,Time Series Analysis and Its Application.New York:Springer-Verlag,2000
3 Hamilton J. Time Series Analysis.Princeton University Press,1994(中译本:刘明志译.时间序列分析,中国科学出版社,1999)
4马克威分析系统使用教程——http://www.tenly.com
5 ARIMA算法模型,维基百科
五实例判断一列数据x是否能用ARIMA算法进行预测,预测接下来的五期数据,现有的数据的数值如下:
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ……. |
| 数值 | -0.109 | 0 | 0.178 | 0.339 | 0.373 | 0.441 | 0.461 | 0.348 | …….. |
| X | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 |
| 数值 | -0.204 | 0.034 | 0.204 | 0.253 | 0.195 | 0.131 | 0.017 | -0.182 | -0.262 |
要用ARIMA算法预测该数据,首先要判断该序列是否是平稳的,可以根据数据画出x的序列图:
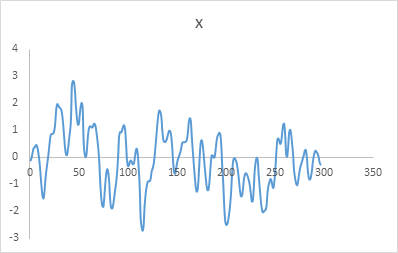
从序列图中可以看出,x的数值大体在坐标轴两侧上下波动,所以说序列x应该是平稳的;
判断序列x是平稳序列之后,下面要分析序列x到底该用哪些模型用来预测,是用AR模型还是MA模型,又或者是两个模型都需要即ARMA模型。我们可以从序列x的自相关系数图和偏自相关系数图是否截尾或拖尾来判断,下面是序列x的自相关和偏自相关图:
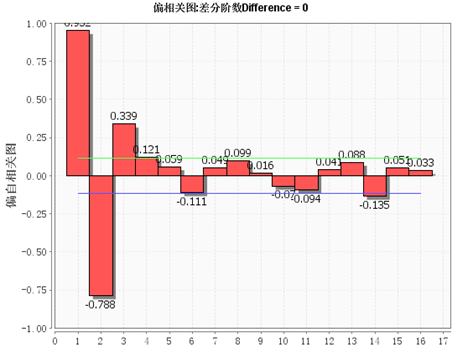
偏自相关图:
自相关图:
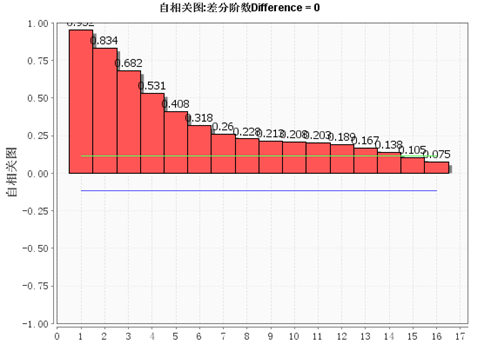
从上面的两个图可以看出:偏自相关图3阶之后的值都在两倍方差之内,所以是截尾的;自相关图是拖尾的,所以模型用AR(3)来预测,即ARIMA模型的参数为(3,0,0);经过计算之后,得到的预测结果如下:
预测的残差平方和=10.498;修正后的R平方=0.9688;这说明模型的拟合度良好,预测的结果准确性比较高。
模型预测的5个值:-0.2617,-0.2159,-0.1639,-0.1120,-0.0712;
拟合-预测图:
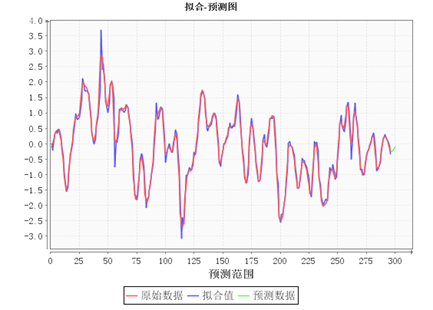 六输入输出
六输入输出
输入变量类型:整型、浮点型(注:参数要求为非负整数)
输入数据尺度:标量型
输出结果:模型的拟合程度,模型的参数估计等。
七相关条目差分原理、平稳数据、随机序列
八优缺点优点:将预测对象随时间推移而形成的数据序列视为一个随机序列,用一定的数学模型来近似描述这个序列。这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值。
缺点:ARIMA模型要求数据具有平稳性,并且需要先对数据进行差分,差分平稳后再建模。
English Box-Jenkins model
French modèle de Box-Jenkins
German Box-Jenkins-Modell
Dutch Box-Jenkins-model
Italian modello Box-Jenkins
Spanish modelo de Box-Jenkins
Romanian modelul Box-Jenkins
Finnish Boxin-Jenkinsin mallit
Turkish Box-Jenkins modeli
Estonian Box-Jenkinsi mudel
Slovenian Box-Jenkinsova model
Polish model Boxa-Jenkinsa
Russian Модель Бокса-Дженкинса
Ukrainian модель Бокса - Дженкінса
Afrikaans Box-Jenkins-model
Chinese 博克斯―詹金斯模型