
一 定义:回归分析(Regression Analysis)是一种统计学上的分析数据的方法,目的在于了解两个或多个变量之间是否相关以及相关方向与强度,并建立数学模型以便观察特定的自变量与需要预测的因变量之间的关系。具体的说,回归分析可以帮助了解在一个或多个自变量变化时因变量的变化量。
二 回归问题的分析方法:1)收集数据;2)建立一个适合相关问题的回归函数;3)通过学习已有的数据,对函数的未知参数进行估计;3)回归方程及回归系数的显著性检验;4)利用这个模型去预测/分类新的数据。
三 回归分析的原理:目的是为了找出一个最能够代表所有观测资料的函数,用这个函数来表示因变量与自变量的关系。回归的基本模型一般可以表示为:Y=f(X ,u),其中Y为因变量,X为自变量,u为未知参数。
四 回归分析方法分类:根据用途可以有多种分类,单变量的线性回归模型,多变量的线性回归模型,广义线性回归模型,概率单位回归模型,逻辑回归模型,曲线回归模型,岭回归模型,主成分回归模型等。
五 回归分析算法背景:
回归分析核心思想是采用最小二乘法原理来求解回归系数,最小二乘法思想背景:1801年,意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。经过40天的跟踪观测后,由于谷神星运行至太阳背后,使得皮亚齐失去了谷神星的位置。随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星,但是根据大多数人计算的结果来寻找谷神星都没有结果。时年24岁的高斯计算了谷神星的轨道并进行了分析。奥地利天文学家海因里希·奥伯斯根据高斯计算出来的轨道重新发现了谷神星。
高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》中,而法国科学家勒让德于1806年独立发现“最小二乘法”,但因不为世人所知而默默无闻。两人曾为谁最早创立最小二乘法原理发生争执。
1829年,高斯提供了最小二乘法的优化效果强于其他方法的证明,见高斯-马尔可夫定理。
六 参考资料:
· 中央大学数学系教材-最小二乘法
· 最小二乘法 - 维基百科,自由的百科全书
· http://www.physics.csbsju.edu/stats/least_squares.html
· http://www.orbitals.com/self/least/least.htm
· PlanetMath上最小二乘法
· 马克威分析系统使用教程——http://www.tenly.com
1.1 算法摘要
主成分回归是指将主成分分析方法用在多元线性回归中的一种回归分析方法。当线性回归模型的自变量存在多重共线性时,主成分回归在不损失大量信息的前提下,降低分析变量的维度,将原来的多个指标组合成少数几个指标,新的指标之间相互独立并且能充分反映总体的信息,以这些新指标为自变量进行多重回归就不会再出现共线性的困扰,便于进一步分析。
主成分回归一般分为两个步骤。第一步,测定主成分数,并通过主成分分析将X降维;第二步,对已经降维的X做线性回归分析。注意,如果在第一步中消去有用的主成分,而保留的是噪声即随机误差,则第二步多元回归所得到的结果就会偏离真实的数学模型。
1.2 算法原理
主成分回归分为确定主成分以及建立线性回归方程这两个部分。首先确定主成分,步骤如下:
1)计算相关系数矩阵和协方差矩阵:
叉积: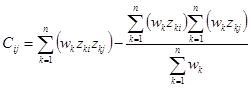
相关系数矩阵: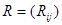 :
: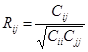
协方差矩阵: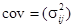 :
: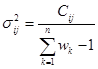
其中Z是数据,w是相应的权重。
2)计算相关系数矩阵或者协方差矩阵的特征根与特征向量:
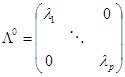 ,
,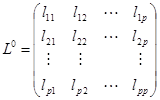
3)根据需求选取最大的前m个特征根与对应的特征向量:
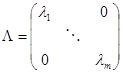 ,
,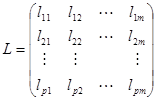
4)计算主成分贡献率及累计贡献率:
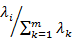 ,
,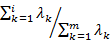
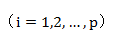
5)计算因子载荷矩阵和共性方差:
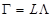 ,
,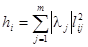
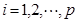
6)计算数据矩阵的列进行标准化:
列均值: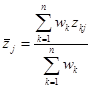 ,
,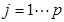
列方差: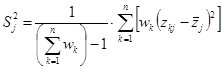 ,
,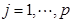
标准化元素: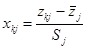 ,
, ,
,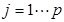

7)计算主成分:
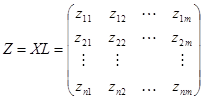
其中L为根据用户需求选取的特征根对应的特征向量。
第二步,确定主成分后,建立回归方程。假设原来的回归模型为:
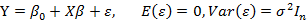
经过第一步确定主成分后,原来的回归方程变为:
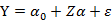
其回归系数就是所谓的主成分估计。而整个过程就称为主成分回归建模。
三相关应用主成分回归分析可应用于:概述数据之间的关系;将原数据转换为互不相关数据;降低数据个数,简化多变量维度;解决回归分析中共线性问题;可用来做一组变量的综合指数等。
可应用的领域:商业(如市场细分)、医学药理分析、化学分析、生物(如农作物生长的影响因素分析)、社会学、地质分析等。
四参考资料1马克威分析系统使用教程——http://www.tenly.com
五实例示例数据为某地抽样调查29名儿童的血红蛋白与4种微量元素的含量数据,现在考虑这四种微量元素钙(X1)、镁(X2)、铁(X3)、铜(X4)能否较好的用来预测血红蛋白的某些指标(Y)的含量。
| 钙 | 镁 | 铁 | 铜 | 血红蛋白 |
| 13.7 | 12.68 | 80.32 | 0.16 | 135 |
| 18.09 | 17.51 | 83.64 | 0.26 | 130 |
| 13.43 | 21.73 | 76.18 | 0.19 | 137.5 |
| 16.15 | 16.1 | 84.09 | 0.19 | 140 |
| 14.67 | 15.48 | 81.72 | 0.16 | 142.5 |
| 10.9 | 10.76 | 70.84 | 0.09 | 127.5 |
| 13.7 | 12.68 | 80.32 | 0.16 | 125 |
| 21.49 | 18 | 78.78 | 0.28 | 122.5 |
| 15.06 | 15.7 | 70.6 | 0.18 | 120 |
| 13.48 | 14.07 | 72.6 | 0.2 | 117.5 |
| 15.28 | 15.35 | 79.83 | 0.22 | 115 |
| 15.01 | 13.84 | 68.59 | 0.14 | 112.5 |
| 17.39 | 16.44 | 74.59 | 0.21 | 111 |
| 18.03 | 16.49 | 77.11 | 0.19 | 107.5 |
| 13.75 | 13.57 | 79.8 | 0.14 | 105 |
| 17.48 | 15.13 | 73.35 | 0.19 | 102.5 |
| 15.73 | 14.41 | 68.75 | 0.13 | 100 |
| 12.16 | 12.55 | 61.38 | 0.15 | 97.5 |
| 13.04 | 11.15 | 58.41 | 0.13 | 95 |
| 13.03 | 14.87 | 69.55 | 0.16 | 92.5 |
| 12.4 | 10.45 | 59.27 | 0.14 | 90 |
| 15.22 | 12.03 | 46.35 | 0.19 | 87.5 |
| 13.39 | 11.83 | 52.41 | 0.21 | 85 |
| 12.53 | 11.99 | 52.38 | 0.16 | 82.5 |
| 16.3 | 12.33 | 55.99 | 0.16 | 80 |
| 14.07 | 12.04 | 50.66 | 0.21 | 78 |
| 16.5 | 13.12 | 61.61 | 0.11 | 75 |
| 18.44 | 13.54 | 55.94 | 0.18 | 72.5 |
| 11.8 | 11.73 | 52.75 | 0.13 | 70 |
假设在主成分中取特征值的贡献率不低于90%,则经过计算后得到的主成分个数为3,且主成分的表达式为:
Z1=0.5011*钙+0.5587*镁+0.428*铁+0.5034*铜
Z2=-0.4285*钙+0.2405*镁+0.7358*铁-0.466*铜
Z3=-0.752*钙+0.2502*镁-0.144*铁+0.5929*铜
最终计算得到的原始变量的回归方程为:
血红蛋白=-2.289*钙+3.847*镁+1.287*铁-14.769*铜
六输入输出输入变量类型:整型、浮点型,数据要求没有缺损
输入数据尺度:标量型
输出结果:得到主成分回归的回归方程
七相关条目主成分分析、相关系数矩阵、协方差矩阵
八优缺点优点:1)可消除评价指标之间的相关影响:主成分分析在对原指标变量进行变换后形成了彼此相互独立的主成分,指标之间相关程度越高,主成分分析效果越好。 2)可减少指标选择的工作量 3)当评级指标较多时还可以在保留绝大部分信息的情况下用少数几个综合指标代替原指标进行分析,减少了计算工作量。 4)在综合评价函数中,各主成分的权数为其贡献率,它反映了该主成分包含原始数据的信息量占全部信息量的比重,这样确定权数是客观的、合理的,它克服了某些评价方法中认为确定权数的缺陷。
缺点:1)在主成分分析中,我们首先应保证所提取的前几个主成分的累计贡献率达到一个较高的水平(即变量降维后的信息量须保持在一个较高水平上)2)对这些被提取的主成分必须都能够给出符合实际背景和意义的解释(否则主成分将空有信息量而无实际含义)3)得到的主元物理意义或者现实含义没有原来的变量那么清晰透彻,而且得到的特征值有负号的时候,综合评价函数意义就不明确。