
一 定义:回归分析(Regression Analysis)是一种统计学上的分析数据的方法,目的在于了解两个或多个变量之间是否相关以及相关方向与强度,并建立数学模型以便观察特定的自变量与需要预测的因变量之间的关系。具体的说,回归分析可以帮助了解在一个或多个自变量变化时因变量的变化量。
二 回归问题的分析方法:1)收集数据;2)建立一个适合相关问题的回归函数;3)通过学习已有的数据,对函数的未知参数进行估计;3)回归方程及回归系数的显著性检验;4)利用这个模型去预测/分类新的数据。
三 回归分析的原理:目的是为了找出一个最能够代表所有观测资料的函数,用这个函数来表示因变量与自变量的关系。回归的基本模型一般可以表示为:Y=f(X ,u),其中Y为因变量,X为自变量,u为未知参数。
四 回归分析方法分类:根据用途可以有多种分类,单变量的线性回归模型,多变量的线性回归模型,广义线性回归模型,概率单位回归模型,逻辑回归模型,曲线回归模型,岭回归模型,主成分回归模型等。
五 回归分析算法背景:
回归分析核心思想是采用最小二乘法原理来求解回归系数,最小二乘法思想背景:1801年,意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。经过40天的跟踪观测后,由于谷神星运行至太阳背后,使得皮亚齐失去了谷神星的位置。随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星,但是根据大多数人计算的结果来寻找谷神星都没有结果。时年24岁的高斯计算了谷神星的轨道并进行了分析。奥地利天文学家海因里希·奥伯斯根据高斯计算出来的轨道重新发现了谷神星。
高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》中,而法国科学家勒让德于1806年独立发现“最小二乘法”,但因不为世人所知而默默无闻。两人曾为谁最早创立最小二乘法原理发生争执。
1829年,高斯提供了最小二乘法的优化效果强于其他方法的证明,见高斯-马尔可夫定理。
六 参考资料:
· 中央大学数学系教材-最小二乘法
· 最小二乘法 - 维基百科,自由的百科全书
· http://www.physics.csbsju.edu/stats/least_squares.html
· http://www.orbitals.com/self/least/least.htm
· PlanetMath上最小二乘法
· 马克威分析系统使用教程——http://www.tenly.com
1.1 算法摘要
岭回归是专门用于共线性数据的有偏估计回归方法。其实质是改良的最小二乘法,以放弃最小二乘的无偏性,损失部分信息,放弃部分精确度为代价来寻求效果稍差,但更符合实际的回归方程。
可应用的情况包括:数据点少于变量个数、所有变量之间有较强的线性相关性、变量之间的数据变化比较小、部分变量之间有线性相关等。
1.2 算法原理
岭回归为了避免最小二乘法中矩阵计算 的行列式接近于零,而使得计算误差太大,所以在矩阵的主对角元素都加上一个K值,降低矩阵计算奇异的风险。矩阵可以表示为:
的行列式接近于零,而使得计算误差太大,所以在矩阵的主对角元素都加上一个K值,降低矩阵计算奇异的风险。矩阵可以表示为:

B(K)为回归方程组 的最小平方解;它的值随着K的改变而改变,这个值就称为岭迹,我们可以根据岭迹图的平稳性确定K的取值。
的最小平方解;它的值随着K的改变而改变,这个值就称为岭迹,我们可以根据岭迹图的平稳性确定K的取值。
所以岭回归主要在于参数K的选取;一般常用的参数选择方法包含以下四种类型:
1)利用方法Hoerl和Kennard(1970):

2)利用方法Lawless和Wang(1975):

3)利用方法Hoerl和Baldwin(1975):

4)利用方法均方误差H(k)最小法:
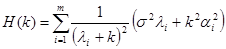
K值选取的原则:尽可能小的k使得参数 的估计值尽量稳定下来。
的估计值尽量稳定下来。
岭回归对参数的估计步骤可以简化为以下几点:
1)对原始模型的变换: ;先对自变量X作中心化和表量化处理,引入新变量Z,令:
;先对自变量X作中心化和表量化处理,引入新变量Z,令:

代入方程可变为:

最后转换得到参数的最小平方估计为:

2)确定合适的K值;
3)确定K值后,参数估计的表达式为:

 三相关应用
三相关应用
岭回归是在自变量组成的信息矩阵的主对角线元素上人为的加入一个非负因子k,使得矩阵行列式不为零,以降低对回归系数估计的误差,提高估计精确度以及模型的平稳性。它是最小二乘法的补充,岭回归可以修复病态矩阵,达到较好的效果。
近年来,岭回归在经济、工业生产、工程技术、环境保护等方面已有一定的应用。
四参考资料1马克威分析系统使用教程——http://www.tenly.com
五实例示例数据:财政收入影响因素分析问题。财政收入(Y)与国民收入(X1)、工业总产值(X2)、农业总产值(X3)、总人口(X4)、就业人口(X5)、固定资产投资(X6)等因素之间的关系。下表为1952年到1981年的原始数据。
1952-1981年财政收入、国民收入、工业总产值、
农业总产值、总人口、就业人口、固定资产投资数据情况
| 年份 | 国民收入(亿元) | 工业总产值(亿元) | 农业总产值(亿元) | 总人口(万人) | 就业人口(万人) | 固定资产投资(亿元) | 财政收入(亿元) |
| 1952 | 598 | 349 | 461 | 57482 | 20729 | 44 | 184 |
| 1953 | 586 | 455 | 475 | 58796 | 21364 | 89 | 216 |
| 1954 | 707 | 520 | 491 | 60266 | 21832 | 97 | 248 |
| 1955 | 737 | 558 | 529 | 61465 | 22328 | 98 | 254 |
| 1956 | 825 | 715 | 556 | 62828 | 23018 | 150 | 268 |
| 1957 | 837 | 798 | 575 | 64653 | 23711 | 139 | 286 |
| 1958 | 1028 | 1235 | 598 | 65994 | 26600 | 256 | 357 |
| 1959 | 1114 | 1681 | 509 | 67207 | 26173 | 338 | 444 |
| 1960 | 1079 | 1870 | 444 | 66207 | 25880 | 380 | 506 |
| 1961 | 757 | 1156 | 434 | 65859 | 25590 | 138 | 271 |
| 1962 | 677 | 964 | 461 | 67295 | 25110 | 66 | 230 |
| 1963 | 779 | 1046 | 514 | 69172 | 26640 | 85 | 266 |
| 1964 | 943 | 1250 | 584 | 70499 | 27736 | 129 | 323 |
| 1965 | 1152 | 1581 | 632 | 72538 | 28670 | 175 | 393 |
| 1966 | 1322 | 1911 | 687 | 74542 | 29805 | 212 | 466 |
| 1967 | 1249 | 1647 | 697 | 76368 | 30814 | 156 | 352 |
| 1968 | 1187 | 1565 | 680 | 78534 | 31915 | 127 | 303 |
| 1969 | 1372 | 2101 | 688 | 80671 | 33225 | 207 | 447 |
| 1970 | 1638 | 2747 | 767 | 82992 | 34432 | 312 | 564 |
| 1971 | 1780 | 3156 | 790 | 85229 | 35620 | 355 | 638 |
| 1972 | 1833 | 3365 | 789 | 87177 | 35854 | 354 | 658 |
| 1973 | 1978 | 3684 | 855 | 89211 | 36652 | 374 | 691 |
| 1974 | 1993 | 3696 | 891 | 90859 | 37369 | 393 | 655 |
| 1975 | 2121 | 4254 | 932 | 92421 | 38168 | 462 | 692 |
| 1976 | 2052 | 4309 | 955 | 93717 | 38834 | 443 | 657 |
| 1977 | 2189 | 4925 | 971 | 94974 | 39377 | 454 | 723 |
| 1978 | 2475 | 5590 | 1058 | 96259 | 39856 | 550 | 922 |
| 1979 | 2702 | 6065 | 1150 | 97542 | 40581 | 564 | 890 |
| 1980 | 2791 | 6592 | 1194 | 98705 | 41896 | 568 | 826 |
| 1981 | 2927 | 6862 | 1273 | 100072 | 73280 | 496 | 810 |
1)首先用普通的回归来建模,其系数的估计方法为最小二乘法;计算得到的回归方程为:
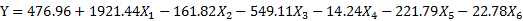
从上述回归方程的系数可以看出,该拟合方程失去了一定的经济意义。这是因为六个变量中只有第一个变量国民收入是正值,其余五个变量的系数均为负值,这明显不符合实际的经济情况。由经济规律可以看出:工业总产值的提高会增加国家的财政税收,因此工业总产值与财政收入应该呈正相关,同样对于农业来说,政府要对农业扶持和实行鼓励政策,当农业总产值升高,政府就会减少对农业的投入,财政收入亦应该提高,这样我们不得不怀疑常回归分析的正确性。
使用岭回归分析,首先要确定岭迹参数k的确定,下图为岭迹图,可以看出当k=0.1时,基本上所有的回归系数的估计值都能达到相对稳定状态。

所以,选定了岭迹参数k之后,计算得到最后的回归方程为:

从岭回归方程可以看出国民收入是影响财政收入的主要因素,其次是固定资产投资;同时工业总产值、农业总产值与财政收入呈现正相关关系,符合实际的经济规律。
六输入输出输入变量类型:整型、浮点型
输入数据尺度:标量型
输出结果:得到岭回归的回归方程
七相关条目最小二乘法、普通线性回归
八优缺点优点:可对变量之间共线性比较严重或病态数据偏多的数据类型作回归分析,对这类数据作回归得到的回归系数更符合实际,更可靠。另外,岭回归能让估计参数的波动范围变小,变的更稳定。
缺点:对系数的估计时,会损失部分信息、降低精度。同时岭回归方程的R平方值会稍低于普通的回归方法。
https://www.zhihu.com/