
一 定义:回归分析(Regression Analysis)是一种统计学上的分析数据的方法,目的在于了解两个或多个变量之间是否相关以及相关方向与强度,并建立数学模型以便观察特定的自变量与需要预测的因变量之间的关系。具体的说,回归分析可以帮助了解在一个或多个自变量变化时因变量的变化量。
二 回归问题的分析方法:1)收集数据;2)建立一个适合相关问题的回归函数;3)通过学习已有的数据,对函数的未知参数进行估计;3)回归方程及回归系数的显著性检验;4)利用这个模型去预测/分类新的数据。
三 回归分析的原理:目的是为了找出一个最能够代表所有观测资料的函数,用这个函数来表示因变量与自变量的关系。回归的基本模型一般可以表示为:Y=f(X ,u),其中Y为因变量,X为自变量,u为未知参数。
四 回归分析方法分类:根据用途可以有多种分类,单变量的线性回归模型,多变量的线性回归模型,广义线性回归模型,概率单位回归模型,逻辑回归模型,曲线回归模型,岭回归模型,主成分回归模型等。
五 回归分析算法背景:
回归分析核心思想是采用最小二乘法原理来求解回归系数,最小二乘法思想背景:1801年,意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。经过40天的跟踪观测后,由于谷神星运行至太阳背后,使得皮亚齐失去了谷神星的位置。随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星,但是根据大多数人计算的结果来寻找谷神星都没有结果。时年24岁的高斯计算了谷神星的轨道并进行了分析。奥地利天文学家海因里希·奥伯斯根据高斯计算出来的轨道重新发现了谷神星。
高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》中,而法国科学家勒让德于1806年独立发现“最小二乘法”,但因不为世人所知而默默无闻。两人曾为谁最早创立最小二乘法原理发生争执。
1829年,高斯提供了最小二乘法的优化效果强于其他方法的证明,见高斯-马尔可夫定理。
六 参考资料:
· 中央大学数学系教材-最小二乘法
· 最小二乘法 - 维基百科,自由的百科全书
· http://www.physics.csbsju.edu/stats/least_squares.html
· http://www.orbitals.com/self/least/least.htm
· PlanetMath上最小二乘法
· 马克威分析系统使用教程——http://www.tenly.com
1.1 算法摘要
广义的线型回归是指参数线型回归(即参数仅以一次方的形式出现在模型中),而解释变量并不一定是线性的。广义线性回归模型的自变量可以是离散的,也可以是连续的;离散的取值可以为二值的,也可为多值的。同时广义回归的随机误差项不一定服从正态分布,可以是其它的指数分布族;也可以服从二项、泊松、负二项伽马等分布。
广义回归模型的建立包含三个部分:选择变量、确定变量之间的数学关系、拟定回归方程中的需要估计参数的数值范围。确定模型中所包含的变量主要是指确定解释变量(因变量);确定模型的数学形式主要是选择适当的数学形式描述变量之间的关系,当事先无法确定模型的数学形式时,可以采用各种可能的形式进行试模拟,选取结果较好的一种数学表达式形式;拟定理论模型中的需要估计参数的范围可以用来检验模型的估计结果。
1.2 算法原理
广义线性模型(generalized liner model,GLM)是为了克服线性回归模型的缺点出现的线性回归模型的推广。其自变量可以是离散的,也可以是连续的。离散的可以是0-1变量,亦或是多种取值的变量。
广义线性回归模型与线性回归模型的区别可以归纳为:
(1)随机误差项不一定服从正态分布。可以服从二项、泊松、负二项、正态、伽马、逆高斯等分布,将上述的分布称为指数分布族。
(2)广义线性回归模型引入了链接函数g()。自变量与因变量通过链接函数产生影响,即Y=g(Xβ),链接函数是单调可导的。常用的链接函数有恒等(Y=Xβ)、对数(Y=ln(Xβ))、幂函数、平方根函数以及逻辑函数等。
链接函数的选择可视情况而定,通常只要符合链接函数的值域包含分布期望值即可;如大家比较熟悉的逻辑回归模型就是使用逻辑链接函数、随机误差项服从二项分布得到的模型。链接函数的参数指数分布一般有:正态、指数、Gamma、逆高斯、卜瓦松、二项式和多项式分布。
典型的链接函数
| 分布 | 名称 | 链接函数 | 均值函数 |
| 正态 | 恒等 |

|
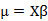
|
| 指数 | 倒数 |
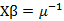
|

|
| Gamma | 逆高斯 | 二次倒数 |
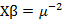
|
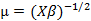
|
卜瓦松 | 自然对数 |
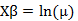
|
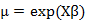
|
二项式 | Logit |
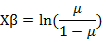
|
1989年,John Nelder和Peter McCullagh首先提出了广义线性回归模型的相关性质。他们在出版的一篇文章中,第一次提出广义线性回归模型的原理、对参数的估计方式(最大似然估计法)以及该模型的实际应用。这篇文献也被认为是广义线性回归模型的代表性资料。
三相关应用广义回归可以应用于经济学数据的预测处理;经济计量研究始于经济学中的理论假设,根据经济理论设定变量间的一组关系,如消费理论、生产理论和各种宏观经济理论;对理论设定的关系进行定量刻画,如消费函数中的边际消费倾向、生产函数中的各种弹性等进行实证研究。
四参考资料1 Nelder JA,WedderburnRWM.Generalied Linear Model.Journal of the Royal Statistical Society A,1972,135:370~384
2 McCullagh P, Nelder JA. Generalied Linear Model.London:Chapmanand Hall,1989
3 DobsonA.An introduction to Generalied Linear Model. London:Chap2manand Hall,1990
4马克威分析系统使用教程——http://www.tenly.com
五实例示例数据为美国消费CS和GDP以及前期消费之间的关系,数据期间为:1947年第1季度-1995年第1季度,共193个数据,数据中已消除了季节因素。数据的具体如下所示:
| Obs | GDP | CS | INV | GOV_NET | P_GDP |
| 1 | 1239.5 | 784 | 43 | 14.7 | 18.3 |
| 2 | 1247.2 | 796.8 | 42.3 | 13.4 | 18.5 |
| 3 | 1255 | 796.7 | 43 | 9.9 | 18.7 |
| 4 | 1269.5 | 795.7 | 49 | 15.4 | 19.3 |
| 5 | 1284 | 803.3 | 49.8 | 13.9 | 19.6 |
| 6 | 1295.7 | 811.6 | 51 | 11.1 | 19.9 |
| 7 | 1303.8 | 814.5 | 51.4 | 7 | 20.3 |
| 8 | 1316.4 | 822.6 | 49.8 | 4.9 | 20.3 |
| 9 | 1305.3 | 823.9 | 43.1 | 0.8 | 20 |
| 10 | 1302 | 834.3 | 35.6 | -3.1 | 19.8 |
| …… | …… | …… | …… | …… | …… |
| 189 | 5261.1 | 3546.34 | 850.2 | -176.2 | 125 |
| 190 | 5314.1 | 3557.841 | 899.3 | -145.1 | 125.9 |
| 191 | 5376 | 3584.728 | 901.5 | -154 | 126.5 |
| 192 | 5433.8 | 3629.591 | 907.9 | -161.1 | 126.9 |
| 193 | 5470 | 3646.104 | 946.5 | -150.3 | 127.6 |
经过计算得到的回归方程为:
消费= -65.849+0.6537*CS+0.2465*GDP
得到了回归方程,可以用来预测未来一段时间的消费水平。如CS增加一个单位的值,消费相应的会增加0.6537个单位,而GDP增加一个单位的值,消费增加0.2465个单位。这就说明CS的值对消费水平的影响更大。
六输入输出输入变量类型:整型、浮点型
输入数据尺度:标量型
输出结果:得到线性回归模型中自变量和因变量之间的回归方程。
七相关条目线性回归、极大似然估计
八优缺点优点:克服了线性回归模型的一些缺点,是对线性回归模型的推广。其自变量可以是离散的,也可以是连续的。并且当事先无法确定模型的数学形式时,可以采用各种可能的形式进行试模拟,选取结果较好的一种数学形式。