
机器学习是一门多领域交叉学科,涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。主要研究计算机怎样模拟或实现人类的学习行为,以获取新的知识和技能,重新组织已有的知识结构,不断的改善自身的性能。
机器学习理论主要是设计和分析一些让计算机可以自动“学习”的算法。这些算法是一类能从数据中自动分析获得规律,并利用规律对未知数据进行预测的算法。简而言之,机器学习主要以数据为基础,通过大数据本身,运用计算机自我学习来寻找数据本身的规律,而这是机器学习与统计分析的基本区别。
机器学习主要有三种方式:监督学习,无监督学习与半监督学习。
(1)监督学习:从给定的训练数据集中学习出一个函数,当新的数据输入时,可以根据函数预测相应的结果。监督学习的训练集要求是包括输入和输出,也就是特征和目标。训练集中的目标是有标注的。如今机器学习已固有的监督学习算法有可以进行分类的,例如贝叶斯分类,SVM,ID3,C4.5以及分类决策树,以及现在最火热的人工神经网络,例如BP神经网络,RBF神经网络,Hopfield神经网络、深度信念网络和卷积神经网络等。人工神经网络是模拟人大脑的思考方式来进行分析,在人工神经网络中有显层,隐层以及输出层,而每一层都会有神经元,神经元的状态或开启或关闭,这取决于大数据。同样监督机器学习算法也可以作回归,最常用便是逻辑回归。
(2)无监督学习:与有监督学习相比,无监督学习的训练集的类标号是未知的,并且要学习的类的个数或集合可能事先不知道。常见的无监督学习算法包括聚类和关联,例如K均值法、Apriori算法。
(3)半监督学习:介于监督学习和无监督学习之间,例如EM算法。
如今的机器学习领域主要的研究工作在三个方面进行:1)面向任务的研究,研究和分析改进一组预定任务的执行性能的学习系统;2)认知模型,研究人类学习过程并进行计算模拟;3)理论的分析,从理论的层面探索可能的算法和独立的应用领域算法。
1.1 算法摘要
自适应提升(AdaBoost:Adaptive Boosting)算法是基于概率近似正确的学习模型下提出的一种提升算法。在分类问题中,AdaBoost通过修改训练样本的权值分布,学习多个弱分类器,并将这些分类器进行线性组合,构成一个强分类器,提高分类性能。其中强分类器可理解为分类精确度高的算法,弱分类器可理解为分类精度低的算法,一般AdaBoost算法是弱分类器的线性组合为:

AdaBoost算法的特点是通过迭代每次学习一个基本分类器(即弱分类器)。每次迭代中,提高那些被前一轮分类器错误分类数据样本的权值,而降低那些被正确分类的数据样本的权值。最后算法将基本分类器的线性组合作为强分类器,其中给分类误差率小的基本分类器以大的权值,给分类误差率大的基本分类器以小的权值。其中极小化损失函数表达式为:

1.2 算法原理
假设给定一个二分类的训练数据集T={(x1,y1),(x2,y2),…,(xn,yn)};其中,每个样本点由实例与标记组成。实例 ,标记
,标记 ,其中X是实例空间,Y是标记集合。AdaBoost算法的原理如下:
,其中X是实例空间,Y是标记集合。AdaBoost算法的原理如下:
输入:训练数据集T={(x1,y1),(x2,y2),…,(xn,yn)};其中 ,
, ;
;
输出:最终的分类器G(x)
(1)初始化训练数据集的权值分布

(2)对于m=1,2,…,M
(a)使用具有权值分布Dm的训练数据集学习,得到基本分类器

(b)计算Gm(x)在训练数据集上的分类误差率

(c)计算Gm(x)的系数
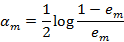
(d)更新训练数据集的权值分布


其中Zm是规范化因子
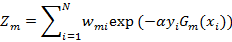
(3)构建基本分类器的线性组合

得到最终分类器为
 二算法背景
二算法背景
1989年,Kearns and Valiant研究概率近似正确学习模型中提出弱学习算法和强学习算法两者的等价问题。即任意给定仅仅比随机猜测稍好的弱学习算法,能否被提升为强学习算法。
1990年,Schapire提出最初的提升算法模型的原型。即弱学习算法可以通过加强提升到一个具有任意高正确率的强学习算法,并通过构造一种多项式级的算法来实现这一个加强过程。
1995年,Freund和Schapire在前人研究的基础上,提出了AdaBoost算法。
三相关应用AdaBoost算法主要用于分类问题。它是通过改变训练样本的权重,学习多个分类器,并将这些分类器线性组合,以提高分类的性能。它的应用范围非常广泛,可用于二分类或多分类的应用场景,可用于特征选择等。
四参考资料1 范明,孟小峰译.数据挖掘:概念与技术.北京:机械工业出版社.2007
2 马克威分析系统使用教程,http://www.tenly.com
3 李航.统计学习方法.北京:清华大学出版社.2012
五实例假定弱分类器由x<v和x>v产生,其阈值v使分类器在数据集上分类误差率最低,使用AdaBoost算法学习一个强分类器。
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 |
初始化数据权值分布
D1=(w11,w12,…,w110),w1i=0.1,i=1,2,…,10
对m=1时,在权值分布为D1的训练数据上,阈值v取2.5时分类误差率最低,故基本分类器为

 在训练数据集上的误差率e1=P(G1(xi)≠yi)=0.3;计算G1(x)的系数:
在训练数据集上的误差率e1=P(G1(xi)≠yi)=0.3;计算G1(x)的系数:

更新训练数据的权值分布:
D2=(w21,…,w2i,…,w210),
计算得到D2的值,且分类器f1(x)=0.4236G1(x);分类器sign[f1(x)]在数据集上有3个误分类点。
对m=2时,在权值分布为D2的训练数据上,阈值v是8.5时分类误差率最低,基本分类器为
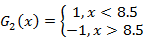
 在训练数据集上的误差率e2=0.2143;计算
在训练数据集上的误差率e2=0.2143;计算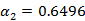
更新训练数据的权值分布:
D3=(w31,…,w3i,…,w310)
计算得到D3的值,且分类器f2(x)=0.4236G1(x)+0.6496G2(x);分类器sign[f2(x)]在训练数据集上有3个误分类点。
对m=3时,在权值分布为D3的训练数据上,阈值v是5.5时分类误差率最低,基本分类器为

 在训练样本集上的误差率为e3=0.182;计算
在训练样本集上的误差率为e3=0.182;计算
更新训练数据的权值分布:
D4=(w41,…,w4i,…,w410)
计算得到D4的值,且分类器f3(x)=0.4236G1(x)+0.6496G2(x)+0.7514G3(x);分类器sign[f3(x)]在训练数据集上误分类点个数为0.
于是最终分类器为
G(x)=sign[f3(x)]=sign[0.4236G1(x)+0.6496G2(x)+0.7514G3(x)]
六输入输出输入数据:数值型数据
输出结果:得到一个分类精度明显提高的强分类器
七相关条目自适应、提升、强学习、弱学习
八优缺点优点:分类精度很高的分类器;弱分类器容易构造;算法简单,不用做特征筛选;不用担心过拟合