机器学习是一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。主要研究计算机怎样模拟或实现人类的学习行为，以获取新的知识和技能，重新组织已有的知识结构，不断的改善自身的性能。
机器学习理论主要是设计和分析一些让计算机可以自动“学习”的算法。这些算法是一类能从数据中自动分析获得规律，并利用规律对未知数据进行预测的算法。简而言之，机器学习主要以数据为基础，通过大数据本身，运用计算机自我学习来寻找数据本身的规律，而这是机器学习与统计分析的基本区别。
机器学习主要有三种方式：监督学习，无监督学习与半监督学习。
（1）监督学习：从给定的训练数据集中学习出一个函数，当新的数据输入时，可以根据函数预测相应的结果。监督学习的训练集要求是包括输入和输出，也就是特征和目标。训练集中的目标是有标注的。如今机器学习已固有的监督学习算法有可以进行分类的，例如贝叶斯分类，SVM，ID3，C4.5以及分类决策树，以及现在最火热的人工神经网络，例如BP神经网络，RBF神经网络，Hopfield神经网络、深度信念网络和卷积神经网络等。人工神经网络是模拟人大脑的思考方式来进行分析，在人工神经网络中有显层，隐层以及输出层，而每一层都会有神经元，神经元的状态或开启或关闭，这取决于大数据。同样监督机器学习算法也可以作回归，最常用便是逻辑回归。
（2）无监督学习：与有监督学习相比，无监督学习的训练集的类标号是未知的，并且要学习的类的个数或集合可能事先不知道。常见的无监督学习算法包括聚类和关联，例如K均值法、Apriori算法。
（3）半监督学习：介于监督学习和无监督学习之间,例如EM算法。
如今的机器学习领域主要的研究工作在三个方面进行：1）面向任务的研究，研究和分析改进一组预定任务的执行性能的学习系统；2）认知模型，研究人类学习过程并进行计算模拟；3）理论的分析，从理论的层面探索可能的算法和独立的应用领域算法。
广义序列模式（简称GSP）算法是Apriori类算法，采用冗余候选模式的剪除策略和特殊的数据结构-哈希树来实现候选模式的快速访存。
GSP算法描述主要包含以下三个步骤：
（1）扫描序列数据库，得到长度为1的序列模式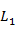
，作为初始的种子集。
（2）根据长度为i的种子集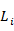
，通过连接操作和修剪操作生成长度为i+1的候选序列模式
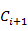，然后扫描序列数据库，计算每个候选序列模式的支持度，产生长度为i+1的序列模式
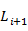，并将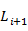作为新的种子集。
（3）重复以上步骤，直到没有新的序列模式或新的候选序列模式产生为止。
GSP产生候选序列模式两个步骤：
（1）连接阶段：当去掉序列模式S1的第一个项目与去掉序列模式S2的最后一个项目所得到的序列相同，则可以将S1和S2进行连接，即将S2的最后一个项目添加到S1中去。
（2）剪枝阶段：若某候选序列模式的某个子集不是序列模式，则此候选序列模式不可能是序列模式，将它从候选序列模式中删除。
GSP算法需要重复的扫描序列数据库，会产生大量的候选集，当序列模式的长度较长的情况下，用GSP处理比较困难。
二算法背景GSP序列模式是由Srikant R和Agrawal R于1996年基于Apriori算法上提出的挖掘序列频繁模式的算法。主要引入3个新概念来定义频繁模式子序列，1）加入时间约束，使得只要满足最小和最大约束，都算是连续的；2）加入时间计算复杂度，控制在一定范围内的都认为在项集中；3）加入分类标准。
三相关应用GSP序列模式算法采用冗余候选模式的减除策略和哈希树来实现候选模式的快速访存。GSP被广泛应用于顾客购买行为的分析、网络访问模式分析、科学实验的分析、疾病治疗的早期诊断、自然灾害的预测、DNA序列的破译等方面。
四参考资料1 R. Srikant and R. Agrawal. Mining Sequential Patterns: Generalizations and Performance Improvements.
2 Bing Liu. <Web Data Exploring Hyperlinks, Contents, and Usage Data>.Second Edition.
3 马克威分析系统使用教程，http://www.tenly.com
五实例给定一个序列数据库S，假设最小支持度计数为2，数据库中项的集合为{a,b,c,d,e,f,g}，数据库中包含4个序列，使用GSP算法产生频繁项集。具体如下表所示
| 序列ID | 序列 |
| 1 | <a(abc)(ac)d(cf)> |
| 2 | <(ad)c(bc)(ae)> |
| 3 | <(ef)(ab)(df)cb> |
| 4 | <eg(af)cbc> |
首先，第一遍扫描数据库，GSP收集每项的支持度。候选序列的集合{<a:4>,<b:4>,<c:3>,<d:3>,<e:3>,<f:3>,<g:1>}。序列g的支持度计数为1，不满足最小支持度计数的序列，所以删除该序列，得到第一个序列的种子集合，即L1={<a>,<b>,<c>,<d>,<e>,<f>}，该集合中的每个元素代表一个1事件序列模式，之后每遍扫描都是基于上一遍扫描发现的种子集开始，并使用它产生新的候选序列，它们都是潜在频繁的。
以L1作种子集，这6个长度为1的序列会产生51个长度2的候选序列的集合C2={<aa>,<ab>,…,<af>,<ba>,<bb>,…,<ff>,<(ab)>,<(ac)>,…,<(ef)>}.
GSP利用先验性质裁剪候选集。在第k遍扫描，一个序列是候选，仅当它的所有长度为(k-1)的子序列都在(k-1)遍扫描发现的序列模式。重新扫描数据库，收集每个候选序列的支持度，并发现新的序列模式集Lk。这个集合变成下次扫描的种子。当一遍扫描不能发现后继序列模式或产生新的候选序列时算法终止。显然，扫描的遍数至少为序列模式的最大长度。如果最后一次扫描得到的序列模式仍产生新的候选序列，则GSP需要再扫描一次。
六输入输出输入数据类型：输入数据类型：数值型数据、字符型数据。（要求输入的数据应满足序列的模式）
输出结果：得到所有的序列模式
七相关条目Apriori、频繁项集、序列
八优缺点优点：由于增加了新的扫描约束条件，有效的减少了需要扫描的候选序列数量，克服了基本序列模型的局限性，减少多余无用模式的产生。GSP用哈希树存储候选序列，减少需要扫描的序列数量，同时对数据序列的表达方式进行了转换，可以更有效的发现一个候选项是否是数据序列的子序列。
缺点：若序列数据库的规模较大，可能会产生大量的候选序列模式，需对数据库进行循环扫描。对序列模式长度较长时，由于产生短的序列模式规模太大，所以算法很难处理这种情况。
