机器学习是一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。主要研究计算机怎样模拟或实现人类的学习行为，以获取新的知识和技能，重新组织已有的知识结构，不断的改善自身的性能。
机器学习理论主要是设计和分析一些让计算机可以自动“学习”的算法。这些算法是一类能从数据中自动分析获得规律，并利用规律对未知数据进行预测的算法。简而言之，机器学习主要以数据为基础，通过大数据本身，运用计算机自我学习来寻找数据本身的规律，而这是机器学习与统计分析的基本区别。
机器学习主要有三种方式：监督学习，无监督学习与半监督学习。
（1）监督学习：从给定的训练数据集中学习出一个函数，当新的数据输入时，可以根据函数预测相应的结果。监督学习的训练集要求是包括输入和输出，也就是特征和目标。训练集中的目标是有标注的。如今机器学习已固有的监督学习算法有可以进行分类的，例如贝叶斯分类，SVM，ID3，C4.5以及分类决策树，以及现在最火热的人工神经网络，例如BP神经网络，RBF神经网络，Hopfield神经网络、深度信念网络和卷积神经网络等。人工神经网络是模拟人大脑的思考方式来进行分析，在人工神经网络中有显层，隐层以及输出层，而每一层都会有神经元，神经元的状态或开启或关闭，这取决于大数据。同样监督机器学习算法也可以作回归，最常用便是逻辑回归。
（2）无监督学习：与有监督学习相比，无监督学习的训练集的类标号是未知的，并且要学习的类的个数或集合可能事先不知道。常见的无监督学习算法包括聚类和关联，例如K均值法、Apriori算法。
（3）半监督学习：介于监督学习和无监督学习之间,例如EM算法。
如今的机器学习领域主要的研究工作在三个方面进行：1）面向任务的研究，研究和分析改进一组预定任务的执行性能的学习系统；2）认知模型，研究人类学习过程并进行计算模拟；3）理论的分析，从理论的层面探索可能的算法和独立的应用领域算法。
1.1 算法摘要
分类回归树(Classification And Regression Tree, CART)模型是决策树学习方法的一种，CART既可以用于分类计算，也可以用于回归。
不同于C4.5，CART本质是对特征空间进行二元划分（即CART生成的决策树是一棵二叉树），并能够对标量属性（nominal attribute）与连续属性（continuous attribute）进行分裂。
1.2 算法原理
CART决策树是结构简洁的二叉树，采用一种二分递归分割的技术，将当前的样本集分为两个子样本集，使得生成的每个非叶子的节点都有两个分支。与普通的决策树算法一样，CART算法包括两个过程：1）决策树的生成：基于训练数据集生成决策树，生成的决策树要尽量的大；2）决策树的剪枝：用验证数据集对以生成的树进行剪枝并选择最优子树，此时用损失函数最小作为剪枝的标准。
1、决策树的生成
决策树的生成就是递归的构建二叉决策树的过程。对回归树用平方误差最小化准则，对分类树用基尼指数最小化原则，进行特征选择，生成二叉树。主要的原理如下：
（1）分类树原理：分类树采用基尼指数（Gini index, Gini）选择最优特征，同时决定该特征的最优二值切分点。基尼指数定义为：
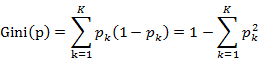
对于给定样本集合D，其基尼指数的计算为：
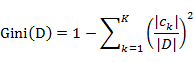
如果样本集合D根据特征A是否取某一可能值a被分割成D1和D2两部分，即：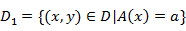
，D2=D-D1
则在特征A的条件下，集合D的基尼指数计算公式为：
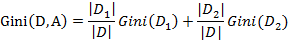
基尼指数Gini(D)表示集合D的不确定性，基尼指数Gini(D,A)表示经A=a分割后集合D的不确定性。基尼指数值越大，样本集合的不确定性也就越大。
（2）回归树原理：回归树用平方误差最小化准则，进行特征选择，生成二叉树。将输入空间划分为M个区域R1，R2，…，Rm，则生成的回归树模型表示为：
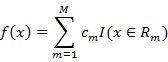
其中cm表示单元Rm上的最小误差平方的最优解。
2、决策树的剪枝
CART算法对于决策树剪枝方法，采用代价复杂度模型，通过交叉验证来估计对预测样本集的误分类损失，产生最小交叉验证误分类估计树。
CART剪枝算法主要由两步组成：首先从生成算法产生的决策树T0底端开始不断剪枝，直到T0的根节点，形成一个子树序列{T0，T1，… ，Tn}；然后通过交叉验证法在独立的验证数据集上对子树序列进行测试，从中选择最优子树。
二算法背景分类与回归树（CART）是由Leo Breiman, Jerome Friedman, Richard Olshen与Charles Stone这四个人于1984年提出，该算法既包含了决策树的构造，又包含相应的分类规则，所以算法既可用于分类也可用于回归。
三相关应用分类回归树本质上也是一种决策树算法；而决策树分类器具有很好的准确性，已被成功的应用于许多的应用领域的分类，如医学、制造和生产、金融分析、天文学与分子生物学等；具体的包括欺诈监测、针对销售、性能预测、制造和医疗整段。决策树是许多商业规则归纳系统的基础。
四参考资料1 李航.统计学习方法.北京：清华大学出版社，2012
2 Pang-Ning Tan, Michael Steinbach, Vipin Kumar, Introduction to Data Mining
3 Dan Steinberg, The Top Ten Algorithms in Data Mining.
4 马克威分析系统使用教程，http://www.tenly.com
五实例示例数据为银行客户贷款申请人的特征数据，其中数据如下：
| ID | 年龄 | 有工作 | 有自己房子 | 贷款情况 | 类别 |
| 1 | 青年 | 否 | 否 | 一般 | 否 |
| 2 | 青年 | 否 | 否 | 好 | 否 |
| 3 | 青年 | 是 | 否 | 好 | 是 |
| 4 | 青年 | 是 | 是 | 一般 | 是 |
| 5 | 青年 | 否 | 否 | 一般 | 否 |
| 6 | 中年 | 否 | 否 | 一般 | 否 |
| 7 | 中年 | 否 | 否 | 好 | 否 |
| 8 | 中年 | 是 | 是 | 好 | 是 |
| 9 | 中年 | 否 | 是 | 非常好 | 是 |
| 10 | 中年 | 否 | 是 | 非常好 | 是 |
| 11 | 老年 | 否 | 是 | 非常好 | 是 |
| 12 | 老年 | 否 | 是 | 好 | 是 |
| 13 | 老年 | 是 | 否 | 好 | 是 |
| 14 | 老年 | 是 | 否 | 非常好 | 是 |
| 15 | 老年 | 否 | 否 | 一般 | 否 |
现在用CART算法生成决策树。
下面是求解过程：
分别以D为数据集，A1,A2,A3,A4表示年龄、有工作、有自己的房子、贷款情况4个特征，并以1，2，3表示年龄为青年、中年和老年，以1，2表示有工作和有自己的房子的值为是和否，以1，2，3表示信贷情况值为非常好、好、一般。
首先计算各个特征的基尼指数，选择最优特征以及其最优切分点。先求特征A的基尼指数：
Gini(D,A1=1)=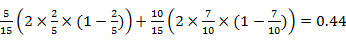
Gini(D,A2=2)=0.48，Gini(D,A3=3)=0.44
由于Gini(D,A1=1)与Gini(D,A3=3)相等且最小，所以A1=1，A1=3都可以选作A1的最优切分点。
求特征A2和A3的基尼指数：
Gini(D,A2=1)=0.32，Gini(D,A3=1)=0.27
由于A2与A3只有一个切分点，所以它们就是最优切分点。
求特征A4的基尼指数：
Gini(D,A4=1)=0.36， Gini(D,A4=2)=0.47， Gini(D,A4=3)=0.32
Gini(D,A4=3)=0.32最小，所以A4=3为A4的最优切分点。
在A1，A2，A3，A4几个特征中，Gini(D,A3=1)=0.27最小，所以选择特征A3为最优特征，A3=1为其最优切分点。于是根节点生成两个子节点，一个是叶节点。对另一个节点继续使用以上方法，在A1，A2，A4中选择最优特征及其最优切分点，结果A2=1.依次计算得知，所有节点都是叶节点。
六输入输出输入变量类型：数值类型、字符型。
输出结果：生成一颗决策树以及给出分类规则
七相关条目决策树、ID3、C4.5、信息增益、基尼指数
八优缺点优点：可以生成易于理解的规则；计算量相对来说不大；可处理连续和离散字段；最终结果可清晰显示字段的重要性程度。
缺点：对连续字段难以预测；处理时间序列数据，前期预处理步骤多；当类别太多，错误可能增加的较快。
