人工神经网络 （Artificial Neural Network，ANN）简称神经网络(NN)，是基于生物学中神经网络的基本原理，在理解和抽象了人脑结构和外界刺激响应机制后，以网络拓扑知识为理论基础，模拟人脑的神经系统对复杂信息的处理机制的一种数学模型，根植于神经科学、数学、思维科学、人工智能、统计学、物理学、计算机科学以及工程科学的一门技术，通常用于解决分类和回归问题。具有并行分布的处理能力、高容错性、智能化和自学习等能力的特征，本质上是一个有大量简单元件相互连接而成的复杂网络，具有高度的非线性，能够进行复杂的逻辑操作和非线性关系实现的系统。
神经网络由大量的节点（或称神经元）之间相互联接构成，每个节点代表一种特定的输出函数，称为激活函数（activation function）；每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重（weight），神经网络就是通过这种方式来模拟人类的记忆。网络的输出则取决于网络的结构、网络的连接方式、权重和激活函数。而网络自身通常都是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达，是对传统逻辑学演算的进一步延伸。
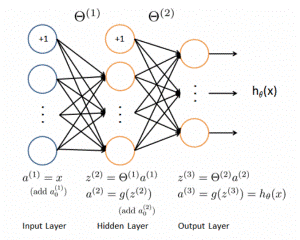
人工神经网络中，神经元处理单元可表示不同的对象，例如特征、字母、概念，或者一些有意义的抽象模式。网络中处理单元的类型分为三类：输入单元、输出单元和隐单元。输入单元接受外部世界的信号与数据；输出单元实现系统处理结果的输出；隐单元是处在输入和输出单元之间，不能由系统外部观察的单元。神经元间的连接权值反映了单元间的连接强度，信息的表示和处理体现在网络处理单元的连接关系中。
算法背景和发展
20世纪40年代，人们开始对神经网络研究。
1943 年，美国心理学家麦克洛奇（Mcculloch）和数学家皮兹（Pitts）提出了M-P模型，此模型比较简单，但是意义重大。在模型中，通过把神经元看作功能逻辑器件来实现算法，从此开创了神经网络模型的理论研究。
1949心理学家赫布（Hebb）提出Hebb法则，为构造有学习功能的神经网络模型奠定了基础。
1957 年，罗森勃拉特（Rosenblatt）以M-P 模型为基础，提出了感知器（Perceptron）模型；
1959年，美国著名工程师威德罗（B.Widrow）和霍夫（M.Hoff）等人提出ADALINE网络模型，ADALINE网络模型是一种连续取值的自适应线性神经元网络模型，可以用于自适应系统。
1972年，芬兰的KohonenT.教授，提出了自组织神经网络SOM(Self-Organizing feature map)。
1976年，美国Grossberg教授提出了著名的自适应共振理论ART(Adaptive Resonance Theory)，其学习过程具有自组织和自稳定的特征。
1982年，美国物理学家霍普菲尔德（Hopfield）提出了一种离散神经网络，即离散Hopfield网络，从而有力地推动了神经网络的研究；
1984年，Hinton与年轻学者Sejnowski等合作提出了Boltzmann机模型；
1986年，儒默哈特（D.E.Ru melhart）等人在多层神经网络模型的基础上，提出了多层神经网络权值修正的反向传播学习算法----BP算法（Error Back-Propagation）；
1988年，Chua和Yang提出了细胞神经网络（CNN）模型；
1994年，廖晓昕关于细胞神经网络的数学理论与基础的提出，带来了这个领域新的进展。通过拓广神经网络的激活函数类，给出了更一般的时滞细胞神经网络(DCNN)、Hopfield神经网络（HNN）、双向联想记忆网络（BAM）模型；
径向基函数（RBF，Radial Basis Function）神经网络，是一种对局部逼近的神经网络。是由J.Moody 和C.Darken于20世纪80年代末提出的一种神经网络，径向基函数方法在某种程度上利用了多维空间中传统的严格插值法的研究成果。在神经网络的背景下，隐藏单元提供一个“函数”集，该函数集在输入模式向量扩展至隐层空间时为其构建了一个任意的“基”；这个函数集中的函数就被称为径向基函数。径向基函数首先是在实多变量插值问题的解中引入的。径向基函数是目前数值分析研究中的一个主要领域之一。
最基本的径向基函数（RBF）神经网络的构成包括三层，其中每一层都有着完全不同的作用。输入层由一些感知单元组成，它们将网络与外界环境连接起来；第二层是网络中仅有的一个隐层，它的作用是从输入空间到隐层空间之间进行非线性变换，在大多数情况下，隐层空间有较高的维数；输出层是线性的，它为作用于输入层的激活模式提供响应。
基本的径向基函数RBF网络是具有单稳层的三层前馈网络。由于它模拟了人脑中局部调整、相互覆盖接受域（或称感受域，Receptive Field）的神经网络结构，因此，RBF网络是一种局部逼近网络，现已证明它能以任意精度逼近任一连续函数。
RBF 神经网络是一种三层前向网络，通过输入层空间到隐含层空间的非线性变换以及隐含层空间到输出层空间的线性变换，实现输入层空间到输出层空间的映射。这两个层间变换参数的学习可以分别进行，使得 RBF 神经网络的学习速度较快且可避免局部极小问题。
RBF(Radial Basis Function，径向基函数)是某种沿径向对称的标量函数，通常定义为空间中一点
到某一中心
之间欧氏距离的单调函数，最常用的径向基函数是高斯函数，形式为：
其中为函数中心向量，
为宽度向量。高斯函数的作用域表现出局部性，即当远离时函数取值较小。
如下图所示，RBF 神经网络的结构从左至右分为三层，依次是输入层、隐含层和输出层：
RBF神经网络结构图
网络的输出如下式所示：
与BP神经网络类似，理论上RBF神经网络对任何非线性连续映射能够用任意精度近似。但RBF神经网络有其自身的特点：
RBF 神经网络结构的物理意义比较明确。RBF 网络可以看成是输入层数据空间（通常是低维空间）到隐含层空间（通常是高维空间）的一种非线性映射，以及隐含层空间到输出层的线性映射。通过选择适当的非线性映射变换 RBF 函数，从而将原低维空间非线性不可分的问题转换成高维空间的近似线性可分的问题。
RBF 神经网络的学习分成两阶段，自组织学习阶段和监督学习阶段。在自组织学习阶段获取隐含层中心，在监督学习阶段获取隐含层到输出层之间的权值，各部分参数都可以快速学习，因此速度较快。
分阶段学习的 RBF 神经网络无局部极小值问题。由于 RBF 神经网络的学习与输入样本聚类中心密切相关，因此 RBF 神经网络比较适合应用于有类别特征的数据。
模型隐含层中心个数设定原则：
由于RBF神经网络的思想是将低维空间非线性不可分问题转换成高维空间线性可分问题，因此隐含层中心个数应该大于输入变量个数，一般设为输入变量个数的 2 倍以上。
由于隐含层中心点坐标代表了输入数据的聚类中心，因此隐含层中心个数应该大于输入数据集的按记录划分的类别个数，这样才能有效提取各种类别输入数据的特征。这需要对输入数据集的业务特征有一定了解，然后给出输入数据类别个数的大致范围。一般设隐含层中心个数为输入数据类别个数的 2 倍以上。
综合以上两个原则设定隐含层中心个数，然后可以根据训练和测试的效果，对中心个数进行适当调整。一般情况下，中心个数设得越多，训练的效果越好，但所需要的时间越长；而当中心个数多到一定程度的时候，增多中心个数对训练效果的改善已不大。另外，隐含层中心数应该不大于训练数据记录数。
二相关应用RBF神经网络能够逼近任意的非线性函数，可以处理系统内的难以解析的规律性，具有良好的泛化能力，并有很快的学习收敛速度，已成功应用于非线性函数逼近、时间序列分析、数据分类、模式识别、信息处理、图像处理、系统建模、控制和故障诊断等。
三参考资料1. Simon Haykin，《神经网络原理》，2004，机械工业出版社
2. 维基百科
3. 百度百科
4. 马克威分析系统使用教程，www.tenly.com
5. Jackson I R H.An order of convergence for some RBFs.IMA J of Numerical Analysis, 1989,9(4):567-587
三参考案例在XOR问题中，有四个二维空间上的点（模式），(1,1)，(0,1), (0,0), (1,0)，现在我们建立一个模式分类器产生二值输出响应，其中点(1,1)，(0,0)对应输出0；(0,1)，(1,0)对应输出1.被研究的RBF网络由一对高斯函数组成，定义如下：
其中中心t1，t2为：
对输出单元的特性做如下假设：
(1) 因问题是对称的，输出单元使用权值共享，这也是先验知识嵌入网络设计的一种形式。虽然有两个隐单元，我们只需确定一个权值w.
(2) 输出单元包含一个偏执b（为独立于数据的变量），此偏执的作用是保证XOR函数具有非零均值的输出。
具体求解过程如下：
五输入输出
√ 特征要求：输入变量和目标变量应该存在因果决定关系，而非毫无关联的随机数据，亦即目标变量应是“可预测”的。
√ 类型要求：数值型，整型或浮点型皆可。
√ 完整要求：计算时程序对样本数据缺失值自动填零。
√ 大小要求：为了充分训练参数，样本数据不宜小于输入变量个数的20倍。
六相关条目人工神经网络，感知机，玻尔兹曼机
七优缺点优点：
1. 它具有唯一最佳的特性，且无局部极小问题存在；
2. RBF神经网络具有较强的输入和输出映射功能，并且理论证明在前向网络中RBF神经网络是完成映射功能的最有效网络；
3. 分类能力好；
4. 学习过程收敛速度快。
缺点：
1. 没有能力来解释自己的推理过程和推理依据；
2. 当样本数据不足时，预测结果不太准确。
