统计，顾名思义即将信息统括起来进行计算的意思，它是对数据进行定量处理的理论与技术。统计分析，常指对收集到的有关数据资料进行整理归类并进行解释的过程。在整个统计分析的过程中，分析是最重要的一个环节，如果缺少这一步，会降低统计工作的作用；准确的说，没有统计分析，统计的工作就没有活力、没有发展，也就没有统计工作的意义。
采用统计分析方法进行研究，必须遵循以下几个统计学基本特征：（1）科学性；（2）直观性；（3）可重复性
统计分析除了基础的统计分析外，还包含了高级统计的知识。高级统计一般包括：回归分析、聚类分析、时间序列、生存分析、判别分析、主成分分析、因子分析、协整分析、联立方程、面板数据模型等统计分析方法。这些高级统计分析不仅包含基础的变量统计信息，还能用于对数据的分类、聚类、回归及预测。可以说高级统计分析部分应用的范围更广、使用频率更高、实际解决问题的能力更强。
统计分析方法很多，但基本方法是定量分析。然而仅仅定量分析还是不足以解决问题，所以应遵循一定的分析技巧，统计分析技巧可以按照“定性—定量—定性”的顺序，巧妙的将定量分析和定性分析结合。
1.1.算法摘要
在现实经济中变量很少处于均衡位置，我们利用变量间的长期均衡关系，测算出协整方程的误差修正，利用记录值的变化对该误差进行回归所得的就是误差修正模型。
系统使用的是约翰逊的约束极大似然算法，并且要区分是否含有常数项和趋势项。
1.2.算法原理
误差修正模型的一般形式为：
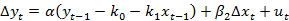
最常用的ECM模型的估计方法是Engle和Granger的两步法，其基本思想是：
第一步是求模型：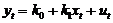
的普通最小二乘法估计，又称协整回归，得到及残差序列：
；
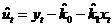第二步是用ut-1替换误差修正模型的一般形式中的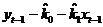
，即对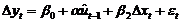
；再用普通最小二乘法的方法估计其参数。
注意，误差修正模型不再单纯地使用变量的水平值（指变量的原始值）或变量的差分建模，而是把两者有机地结合在一起，充分利用这两者所提供的信息。
二算法背景误差修正模型（error correction model，简记为ECM）是一种具有特定形式的计量经济学模型，它的主要形式是由Davidson、 Hendry、Srba和Yeo于1978年提出的，也称为DHSY模型。
三相关应用误差修正模型可以应用于时间经济领域的任何数据，它即能反映不同的时间序列间的长期均衡关系，又能反映短期偏离向长期均衡修正的机制。
根据Engle定理，如果一组变量之间有协整关系，则协整回归总是能被转换为误差修正模型（ECM：Error Correction Model）。协整关系只是反映了变量之间的长期均衡关系，误差修正模型的使用就是为了建立短期的动态模型以弥补长期静态模型的不足。
四参考资料1.维基百科；
2.百度；
3.MBA智库百科（http://wiki.mbalib.com/）
4.马克威分析系统使用教程，www.tenly.com。
5.计量经济学.协整与误差修正模型.华南师范大学教材
五实例假设一列数据表示的是中国历年的宏观经济数据，该数据包含国内生产总值、居民消费总额和投资总额，政府消费。下面用误差修正模型检验国内生产总值与投资是否存在协整的关系。
| 年份 | 国内生产总值 | 消费 | 投资 | 政府支出 |
| 1978 | 3605.6 | 1759.1 | 1377.9 | 468.6 |
| 1979 | 4074 | 2005.4 | 1474.2 | 594.4 |
| 1980 | 4551.3 | 2317.1 | 1590 | 644.2 |
| 1981 | 4901.4 | 2604.1 | 1581 | 716.3 |
| 1982 | 5489.2 | 2867.9 | 1760.2 | 861.1 |
| 1983 | 6076.3 | 3182.5 | 2005 | 888.8 |
| 1984 | 7164.4 | 3674.5 | 2468.6 | 1021.3 |
| 1985 | 8792.1 | 4589 | 3386 | 817.1 |
| 1986 | 10132.8 | 5175 | 3846 | 1111.8 |
| 1987 | 11784.7 | 5961.2 | 4322 | 1501.5 |
| 1988 | 14704 | 7633.1 | 5495 | 1575.9 |
| 1989 | 16466 | 8523.5 | 6095 | 1847.5 |
| 1990 | 18319.5 | 9113.2 | 6444 | 2762.3 |
| 1991 | 21280.4 | 10315.9 | 7517 | 3447.5 |
| 1992 | 25863.7 | 12459.8 | 9636 | 3767.9 |
| 1993 | 34500.7 | 15682.4 | 14998 | 3820.3 |
| 1994 | 46690.7 | 20809.8 | 19260.6 | 6620.3 |
| 1995 | 58510.5 | 26944.5 | 23877 | 7689 |
| 1996 | 68330.4 | 32152.3 | 26867.2 | 9310.9 |
| 1997 | 74894.2 | 34854.6 | 28457.6 | 11582 |
| 1998 | 79003.3 | 36921.1 | 29545.9 | 12536.3 |
| 1999 | 82673.1 | 39334.4 | 30701.6 | 12637.1 |
| 2000 | 89340.9 | 42895.6 | 32499.8 | 13945.5 |
| 2001 | 98592.9 | 45898.1 | 37460.8 | 15234 |
| 2002 | 107514.2 | 48534.5 | 42355.4 | 16624.3 |
最后拟合得到的结果如下所示：
| 对数似然值 | -352.0381 |
| 赤池信息量（AIC） | 33.2762 |
| 施瓦茨信息量（SCI） | 33.9705 |
从拟合准则表可以看出国内生产总值与投资和政府支出具有长期协整关系，上面是误差修正模型中，差分项反应了短期波动的影响，国内生产总值的短期变动可以分为两部分，一部分是短期投资波动的影响，一部分是偏离长期均衡的影响。
六输入输出输入变量类型：要求数值型变量；如：整型、浮点型
输出结果：给出计算结果的统计量。
七相关条目协整关系、时间序列、平稳性检验
八优缺点误差修正模型有许多明显的优点：如 a）一阶差分项的使用消除了变量可能存在的趋势因素，从而避免了虚假回归问题； b）一阶差分项的使用也消除模型可能存在的多重共线性问题； c）误差修正项的引入保证了变量水平值的信息没有被忽视； d）由于误差修正项本身的平稳性，使得该模型可以用经典的回归方法进行估计，尤其是模型中差分项可以使用通常的t检验与F检验来进行选取。
因此，建立误差修正模型，需要首先对变量进行协整分析，以发现变量之间的协整关系，即长期均衡关系，并以这种关系构成误差修正项。 然后建立短期模型，将误差修正项看作一个解释变量，连同其它反映短期波动的解释变量一起，建立短期模型，即误差修正模型。
