统计，顾名思义即将信息统括起来进行计算的意思，它是对数据进行定量处理的理论与技术。统计分析，常指对收集到的有关数据资料进行整理归类并进行解释的过程。在整个统计分析的过程中，分析是最重要的一个环节，如果缺少这一步，会降低统计工作的作用；准确的说，没有统计分析，统计的工作就没有活力、没有发展，也就没有统计工作的意义。
采用统计分析方法进行研究，必须遵循以下几个统计学基本特征：（1）科学性；（2）直观性；（3）可重复性
统计分析除了基础的统计分析外，还包含了高级统计的知识。高级统计一般包括：回归分析、聚类分析、时间序列、生存分析、判别分析、主成分分析、因子分析、协整分析、联立方程、面板数据模型等统计分析方法。这些高级统计分析不仅包含基础的变量统计信息，还能用于对数据的分类、聚类、回归及预测。可以说高级统计分析部分应用的范围更广、使用频率更高、实际解决问题的能力更强。
统计分析方法很多，但基本方法是定量分析。然而仅仅定量分析还是不足以解决问题，所以应遵循一定的分析技巧，统计分析技巧可以按照“定性—定量—定性”的顺序，巧妙的将定量分析和定性分析结合。
1.1.算法摘要
有些时间序列，虽然自身非平稳，但其线性组合却是平稳的；非平稳时间序列的线性组合如果是平稳的，则这种组合反映了变量之间长期稳定的比例关系就称为协整关系。所以我们称检验序列是否存在这种协整关系的检验就叫做协整检验。
有时非平稳序列很可能出现伪回归，协整的意义就是检验它们的回归方程所描述的因果关系是否是伪回归，即检验变量之间是否存在稳定的关系。所以，非平稳序列的因果关系检验就是协整检验。
1.2.算法原理
协整检验从检验的对象上可分为两种：一种是基于回归系数的协整检验，另一种是基于回归残差的协整检验，如ADF检验，残差的协整检验简单而实用，是普遍使用的方法。
Engle和 Granger 1987年提出了残差协整检验方法。其理论根据是，自变量和因变量之间存在协整关系，也就是说，因变量能被自变量的线性组合所解释，两者之间存在稳定的均衡关系，因变量不能被解释部分构成一个残差序列，这个残差序列应该是平稳的。因此，检验一组变量（因变量和解释变量）之间是否存在协整关系等价于检验回归方程残差序列是否是一个平稳序列。通常可以用ADF检验来判断残差的平稳性（单位根检验），进而判断因变量和解释变量之间的协整关系是否存在。
残差单位根检验步骤如下：
第一步：若k个序列y1和y2,y3,…，yk都是1阶单整序列，建立回归方程
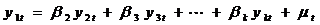
模型估计的残差为
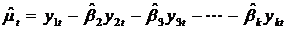
第二步：检验残差序列ut是否平稳，也就是判断序列ut是否含有单位根。通常用ADF检验来判断残差序列是否有单位根。
第三步：如果残差序列是平稳的，则可以确定回归方程中的k个变量（y1,y2,…，yk）之间存在协整关系，并且协整向量为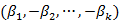
，其中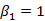
；否则（y1,y2,…，yk）之间不存在协整关系。
协整检验的目的是决定一组非平稳序列的线性组合是否具有协整关系，也可以通过协整检验来判断线性回归方程设定的是否合理，这两者的检验思想和过程是完全相同的。利用ADF检验来判断残差序列是否平稳，进而确定回归变量之间是否存在协整关系，同时还可以判断模型设定是否正确。这是因为，如果残差序列是一个非平稳序列，则说明因变量除了能被解释变量解释的部分以外，其余部分的变化仍然不规则，也就是说回归方程的因变量和解释变量之间不存在稳定的均衡关系，这样的模型有可能拟合度很高、显著性水平等指标都很好，但不能用来预测未来信息，因此称为伪回归。
二算法背景协整思想萌芽于1978年（Davison，Hendry，Srba和Yeo），在1980年代中后期被Granger（1983）、Engle和Granger（1987）所明确发展起来。
1999年，Kao等利用推广的DF和ADF检验提出了检验面板协整的方法，这种方法的零假设是没有协整关系，并利用静态面板回归的残差来构建统计量。
1999年，Pedron在零假设是在动态面板回归中没有协整关系的条件下给出了七种基于残差的面板检验方法。与Kao的方法不同的是，Pedron的检验方法允许异质面板的存在。
2001年，Larssonetal发展了基于Johansen（1995）向量自回归的似然检验的面板协整检验方法，这种检验的方法是检验变量存在共同的协整的秩。
三相关应用协整检验分析可以应用于经济等领域的检验分析；也可用于检验非稳定的时间序列，观察他们是否有一定的线性组合使得该时间序列成为平稳序列。
协整分析是在时间序列的向量自回归分析的基础上发展起来的空间结构与时间动态相结合的建模方法与理论分析方法。与传统的以最小二乘法为基础的线性回归分析相比，在统计上更严格，更具逻辑性。
四参考资料1.维基百科；
2.百度；
3.MBA智库百科（http://wiki.mbalib.com/）
4.马克威分析系统使用教程，www.tenly.com。
5.计量经济学基础（第五版），达摩达尔·N·古扎拉蒂著，中国人民大学出版社。
五实例假设一列数据表示的是中国历年的宏观经济数据，该数据包含国内生产总值、居民消费总额和投资总额，政府消费。下面用协整检验检验国内生产总值与投资是否存在协整的关系。
| 年份 | 国内生产总值 | 消费 | 投资 | 政府支出 |
| 1978 | 3605.6 | 1759.1 | 1377.9 | 468.6 |
| 1979 | 4074 | 2005.4 | 1474.2 | 594.4 |
| 1980 | 4551.3 | 2317.1 | 1590 | 644.2 |
| 1981 | 4901.4 | 2604.1 | 1581 | 716.3 |
| 1982 | 5489.2 | 2867.9 | 1760.2 | 861.1 |
| 1983 | 6076.3 | 3182.5 | 2005 | 888.8 |
| 1984 | 7164.4 | 3674.5 | 2468.6 | 1021.3 |
| 1985 | 8792.1 | 4589 | 3386 | 817.1 |
| 1986 | 10132.8 | 5175 | 3846 | 1111.8 |
| 1987 | 11784.7 | 5961.2 | 4322 | 1501.5 |
| 1988 | 14704 | 7633.1 | 5495 | 1575.9 |
| 1989 | 16466 | 8523.5 | 6095 | 1847.5 |
| 1990 | 18319.5 | 9113.2 | 6444 | 2762.3 |
| 1991 | 21280.4 | 10315.9 | 7517 | 3447.5 |
| 1992 | 25863.7 | 12459.8 | 9636 | 3767.9 |
| 1993 | 34500.7 | 15682.4 | 14998 | 3820.3 |
| 1994 | 46690.7 | 20809.8 | 19260.6 | 6620.3 |
| 1995 | 58510.5 | 26944.5 | 23877 | 7689 |
| 1996 | 68330.4 | 32152.3 | 26867.2 | 9310.9 |
| 1997 | 74894.2 | 34854.6 | 28457.6 | 11582 |
| 1998 | 79003.3 | 36921.1 | 29545.9 | 12536.3 |
| 1999 | 82673.1 | 39334.4 | 30701.6 | 12637.1 |
| 2000 | 89340.9 | 42895.6 | 32499.8 | 13945.5 |
| 2001 | 98592.9 | 45898.1 | 37460.8 | 15234 |
| 2002 | 107514.2 | 48534.5 | 42355.4 | 16624.3 |
我们使用ADF检验，分别计算相关的F统计量及其它参数，结果如下所示：
|
|
特征值 | 检验统计量 | 临界值（5%） |
| 无协整关系 | 0.3270 | 9.4453 | 12.3209 |
| 至多一个 | 0.0328 | 0.7327 | 4.1299 |
由检验统计量F=9.4453<临界值=12.3209；故拒绝原假设，认为国内生产总值与投资存在协整的关系。
六输入输出输入变量类型：要求数值型变量；如：整型、浮点型
输出结果：协整检验的各类统计量
七相关条目时间序列、格兰杰因果检验、单位根检验
八优缺点协整即存在共同的随机性趋势。协整检验的目的是决定一组非平稳序列的线性组合是否具有稳定的均衡关系，伪回归的一种特殊情况即是两个时间序列的趋势成分相同，此时可能利用这种共同趋势修正回归使之可靠。正是由于协整传递出了一种长期均衡关系，若是能在看来具有单独随机性趋势的几个变数之间找到一种可靠联系，那么通过引入这种“相对平稳”对模型进行调整，可以排除单位根带来的随机性趋势，在进行时间系列分析时，传统上要求所用的时间系列必须是平稳的，即没有随机趋势或确定趋势，否则会产生“伪回归”问题。但是，在现实经济中的时间系列通常是非平稳的，我们可以对它进行差分把它变平稳，但这样会让我们失去总量的长期信息，而这些信息对分析问题来说又是必要的，所以用协整来解决此问题。
