统计，顾名思义即将信息统括起来进行计算的意思，它是对数据进行定量处理的理论与技术。统计分析，常指对收集到的有关数据资料进行整理归类并进行解释的过程。在整个统计分析的过程中，分析是最重要的一个环节，如果缺少这一步，会降低统计工作的作用；准确的说，没有统计分析，统计的工作就没有活力、没有发展，也就没有统计工作的意义。
采用统计分析方法进行研究，必须遵循以下几个统计学基本特征：（1）科学性；（2）直观性；（3）可重复性
统计分析除了基础的统计分析外，还包含了高级统计的知识。高级统计一般包括：回归分析、聚类分析、时间序列、生存分析、判别分析、主成分分析、因子分析、协整分析、联立方程、面板数据模型等统计分析方法。这些高级统计分析不仅包含基础的变量统计信息，还能用于对数据的分类、聚类、回归及预测。可以说高级统计分析部分应用的范围更广、使用频率更高、实际解决问题的能力更强。
统计分析方法很多，但基本方法是定量分析。然而仅仅定量分析还是不足以解决问题，所以应遵循一定的分析技巧，统计分析技巧可以按照“定性—定量—定性”的顺序，巧妙的将定量分析和定性分析结合。
1.1.算法摘要
联立方程模型是描述各种不同经济变量之间相互联系方式的方程系统。也就是说联立方程可以用来描述变量之间的多向因果关系，这些变量之间的关系是相互依存、相互交错、多想或多向因果关系。
1.2.算法原理
一般的联立方程系统形式是
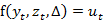t =1， 2， ¼， T
其中：yt 是内生变量向量，zt 是外生变量向量，ut 是一个可能存在序列相关的扰动项向量，T 表示样本容量。估计的任务是寻找未知参数向量 D 的估计量。
内生变量是指在联立方程中，每个相互或共同依赖的变量；每个内生变量都要由一个方程表示，内生变量影响系统且受系统影响，与外生变量的最大区别是，它是具有某种概率分布的随机变量。内生变量是被研究系统的内在组成部分，也是联立方程系统内在决定的。内生变量一般都是经济变量。
外生变量一般是确定性变量，其变化不是由联立方程系统决定的。外生变量是联立方程系统外决定的变量，影响系统但本身不受系统的影响。外生变量一般是经济变量、条件变量、政策变量和虚拟变量。
在进行联立方程估计前首先要判断它是否可以估计，这就是联立方程的识别。
方程中每个需要估计其参数的随机方程都存在识别问题。如果一个模型中的所有随机方程是可以识别的，则认为该联立方程是可以识别的。反过来，只要存在一个不可识别的随机方程，就认为该联立方程是不可识别的。
如果方程的结构式参数存在惟一的估计量，称这个方程为恰好识别；如果某一方程具有多组参数估计量，称其为过渡识别。
1）结构式联立方程的识别条件
假定联立方程结构式：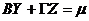
中的第i个方程中包含
个内生变量（含被解释变量）和
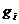个先决变量（含常数项），系统中的内生变量和先决变量的数目用
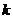和
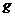表示，矩阵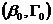
表示第i个方程中未包含的变量（包括内生变量和先决变量），在其他k-1个方程中对应系数所组成的矩阵。于是，判断第i个结构方程识别状态的结构式识别条件为
如果rank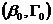<k-1，则第i个方程不可识别；如果rank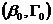=k-1，则第i个方程可以识别，并且如果
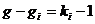，则第 i 个结构方程恰好识别；如果
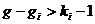，则第i 个结构方程过渡识别。式中：符号rank()表示矩阵的秩。
2）简化式的识别条件
联立方程系统的简化式识别条件，是根据联立方程系统的简化式结构参数进行判断的。简化式模型
简化式识别条件为：
如果rank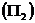
<
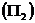，则第 i个结构方程不可识别；如果rank=，则第 i个结构方程可以识别，并且如果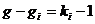，则第i 个结构方程恰好识别；如果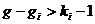，则第i个结构方程过渡识别。
式中：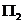
是简化式参数矩阵
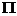中划去第i个结构方程所不包含的内生变量所对应的行和第i个结构方程中包含的先决变量所对应的列之后，剩下的参数按原次序组成的矩阵。其他符号、变量的含义与结构式识别条件相同。
联立方程系统的估计方法分为两种，单方程估计方法与系统估计方法。联立方程的单方程估计方法主要有：间接最小二乘法、工具变量法、两阶段最小二乘法；联立方程的系统估计方法主要有：三阶段最小二乘法、全信息极大似然方法。
二算法背景20世纪30年代，萨缪尔森和希克斯最先研究应用联立方程描述经济变量的行为。这是因为经济学家认为联立方程比只用文字更能精确的描述经济行为，用文字描述涉及众多个人及企业的复杂经济变量之间的关系过于困难。
20世纪六七十年代，诺贝尔经济学奖获得者杰勒德·德布鲁和肯尼斯·J·阿罗把拓扑学引入数量经济学中，从而扩充了联立方程的使用范围，但也使其变得更复杂。后来，青木正直在经济学应用中把最佳控制理论引入联立方程，从而得到进一步的发展。
到20世纪九十年代早期，优秀的经济杂志中至少有60%的论文都包含联立方程，可以说越来越多的经济学家都在用它来研究经济行为。
三相关应用联立方程一般应用于经济领域中，以研究经济变量的行为。经济学家主要在两个方面应用联立方程：一类模型表示如价格水平、价格变化率、供给数量、需求数量之间的经济变量在不同时间点上的互相联系方式；另一类表示经济变量随时间演变的方式。
其中每一类都可以分为线性与非线性模型、连续时间模型与离散时间模型、随机模型和非随机模型。
四参考资料1.维基百科；
2.百度；
3.MBA智库百科（http://wiki.mbalib.com/）
4.马克威分析系统使用教程，www.tenly.com。
5. 结构方程模型与联立方程模型的比较，贾新明，刘亮，《数理统计与管理》2008, 27(3):439-446
五实例数据是美国1954年到1984年的经济发展的数据及各个指标，该数据名为克莱恩联立方程系统。下面以联立方程模型分析这些数据。
| obs | CS | G | I | K | P | R | T | WG | WP | Y |
| 1954 | 370 | 96.1 | 83.1 | 738.8 | 65 | 1.59 | 17 | 47.2 | 427 | 556.1 |
| 1955 | 394.1 | 88.2 | 103.8 | 842.6 | 80.9 | 2.19 | 18.1 | 45.9 | 448.6 | 593.4 |
| 1956 | 405.4 | 86.8 | 102.6 | 945.2 | 79 | 3.31 | 18.5 | 45.6 | 461.8 | 604.9 |
| 1957 | 413.8 | 90.6 | 97 | 1042.2 | 74.1 | 3.82 | 18.8 | 45.8 | 474.6 | 613.3 |
| 1958 | 418 | 93.4 | 87.5 | 1129.7 | 63.4 | 2.47 | 18 | 44.5 | 478.5 | 604.5 |
| 1959 | 440.4 | 91.4 | 108 | 1237.7 | 77.8 | 3.96 | 18.6 | 44.5 | 501.5 | 643.5 |
| 1960 | 452 | 90.4 | 104.7 | 1342.4 | 72.5 | 3.85 | 20.1 | 45.2 | 517 | 654.8 |
| 1961 | 461.4 | 95.3 | 103.9 | 1446.3 | 71.7 | 2.96 | 20.2 | 46.2 | 530.9 | 669 |
| 1962 | 482 | 102.8 | 117.6 | 1563.9 | 77.9 | 3.26 | 21.5 | 48.3 | 562.2 | 709.9 |
| 1963 | 500.5 | 101.8 | 125.1 | 1689 | 83.2 | 3.56 | 22.6 | 48.2 | 582.8 | 736.8 |
| 1964 | 528 | 100.2 | 133 | 1822 | 91.4 | 3.96 | 22.5 | 48.5 | 611.6 | 774 |
| 1965 | 557.5 | 100.3 | 151.9 | 1973.9 | 103.8 | 4.38 | 22.5 | 48.7 | 644.8 | 819.8 |
| 1966 | 585.7 | 112.6 | 163 | 2136.9 | 108.1 | 5.55 | 20.7 | 53 | 686 | 867.8 |
| 1967 | 602.7 | 125.1 | 154.9 | 2291.8 | 100.8 | 5.11 | 21 | 57.2 | 709.1 | 888.1 |
| 1968 | 634.4 | 128.1 | 161.6 | 2453.4 | 107.2 | 5.9 | 21.8 | 58 | 739 | 926 |
| 1969 | 657.9 | 121.8 | 171.4 | 2624.8 | 99.9 | 7.83 | 21.7 | 58.2 | 772.2 | 952 |
| 1970 | 672.1 | 110.6 | 158.5 | 2783.3 | 82.4 | 7.71 | 21.1 | 55.2 | 786.3 | 945.1 |
| 1971 | 696.8 | 103.7 | 173.9 | 2957.2 | 90.4 | 5.11 | 21.1 | 52.5 | 812 | 976.1 |
| 1972 | 737.1 | 101.7 | 195 | 3152.2 | 100.6 | 4.73 | 19.9 | 50.1 | 864 | 1034.6 |
| 1973 | 767.9 | 95.9 | 217.5 | 3369.7 | 118.8 | 8.15 | 19.9 | 48.2 | 910 | 1096.8 |
| 1974 | 762.8 | 96.6 | 195.5 | 3565.2 | 118.8 | 9.84 | 18.9 | 48.5 | 896.6 | 1082.7 |
| 1975 | 779.4 | 97.4 | 154.8 | 3720 | 105 | 6.32 | 11.3 | 48.4 | 899 | 1063.7 |
| 1976 | 823.1 | 96.8 | 184.5 | 3904.5 | 125.7 | 5.34 | 17.7 | 48.5 | 938 | 1129.8 |
| 1977 | 864.3 | 100.4 | 214.2 | 4118.7 | 139 | 5.61 | 17.8 | 48.6 | 995.4 | 1200.9 |
| 1978 | 903.2 | 100.3 | 236.7 | 4355.4 | 152.3 | 7.99 | 18.7 | 49.3 | 1043.9 | 1264.2 |
| 1979 | 927.6 | 102.1 | 236.3 | 4591.7 | 154.6 | 10.91 | 18.4 | 49 | 1081.2 | 1303.2 |
| 1980 | 931.8 | 106.4 | 208.5 | 4800.2 | 131.5 | 12.29 | 22.8 | 49.6 | 1093.2 | 1297 |
| 1981 | 950.5 | 110.3 | 230.9 | 5031.1 | 113.1 | 14.76 | 31.3 | 50 | 1141.1 | 1335.5 |
| 1982 | 963.3 | 117 | 194.3 | 5225.4 | 79.6 | 11.89 | 24.1 | 50.5 | 1150 | 1304.2 |
| 1983 | 1009.2 | 116.2 | 221 | 5446.4 | 94.4 | 8.81 | 24.3 | 51.3 | 1189 | 1359 |
| 1984 | 1062.4 | 122.5 | 289.9 | 5736.3 | 105.5 | 10.16 | 24.8 | 51.9 | 1277.5 | 1459.7 |
应用二阶段最小二乘法分析这些数据，且有数据构成的方程为：
cs=c(10)+c(11)*(wp+wg) +c(12)* r(-1) +c(13)*cs(-1)
I=c(21)*k + c(22)*r(-1) +c(23)*p
wp=c(32)*y+ c(33)*y(-1)+ c(34)*k
经计算得到第一个方程的估计系数为：
c(10)=-20.402，c(11)=0.493，c(12)=-4.278，c(13)= 0.471
第二个方程的估计系数为：
c(21)=0.024，c(22)=0.439，c(23)=0.931
第三个方程的估计系数为：
c(32)=0.728，c(33)=-0.038，c(34)=0.0436
但是方程2的D-W统计量=0.7726，方程3的D-W统计量=0.625；所以方程2和方程3存在序列相关，为了消除这种相关性，可以再方程后加入自回归误差项消除。新的方程组建立如下：
cs=c(10)+c(11)*(wp+wg) +c(12)* r(-1) +c(13)*cs(-1)
I=c(21)*k + c(22)*r(-1) +c(23)*p+[AR(1)=C(25)]
wp=c(32)*y+ c(33)*y(-1)+ c(34)*k+[AR(1)=C(35)]
经计算得到第一个方程的估计系数为：
c(10)=-20.402，c(11)=0.493，c(12)=-4.278，c(13)= 0.471
第二个方程的估计系数为：
c(21)=0.0497，c(22)=-6.716，c(23)=0.554，c(25)=0.854
第三个方程的估计系数为：
c(32)=0.621，c(33)=0.022，c(34)=0.059，c(35)=0.861
加入自回归误差项后，方程2和方程3的D-W统计量分别为：1.7869和1.9313，这表示方程的系数估计很好。
六输入输出输入变量类型：要求数值型变量；如：整型、浮点型
输出结果：联立方程系数估计的各个统计量。
七相关条目时间序列、间接最小二乘法、工具变量法、两阶段最小二乘法、三阶段最小二乘法、全信息极大似然方法
八优缺点1.联立方程无法处理潜变量问题；
2.变量的忽略（遗漏），一般会造成参数和方差-协方差矩阵的非一致估计，而变量的忽略是模型设定中比较严重的缺陷；
3.联立方程的正则假设中，变量均被看做是不存在测量误差，在现实中很多变量都是不能直接地准确测量。
